Relatório 5 - SOAR: Tutoriais 4 e 5

Sumário

• Exercício 1
• Exercício 2
  • O problema Water Jug (jarro d'água)
  • O problema Missionários e Canibais

Exercício 1

Nesse exercício é apresentado soluções para um problema semelhante ao Water Jug, visto no tutorial 1, onde é necessário trabalhar com busca interna. O problema abordado no exercício é o "Missionários e Canibais" (Missionaries and Cannibals), que pode ser definido da seguinte forma:

• Três missionários e três canibais precisam atravessar um rio. Há um barco na margem do rio que pode ser usado por eles para atravessá-lo, desde que o número de canibais nunca supere o número de missionários em qualquer margem do rio, pois se isso acontecer, os canibais irão se alimentar dos missionários. Uma ou duas pessoas podem usar o barco ao mesmo tempo. Como os missionários e canibais podem atravessar o rio com sucesso?

Representação do estado

A primeira coisa a se fazer para resolver o problema Missionários e Canibais é definir quais partes do problema devem ser representadas no estado. Dada a descrição do problema, sabe-se que os seguintes objetos devem ser descritos: três missionários, três canibais, um rio e um barco. É necessário definir também, durante a solução do problema, em que margem do rio está o barco e a quantidade de canibais e missionários em cada margem. Uma das formas de representar o estado é criar duas estruturas que representem as margens do rio. Em casa uma dessas estruturas, é definido os seguintes argumentos: número de canibais, número de missionários, barco e outra-margem. Esse último argumento foi colocado para facilitar a identifição da outra margem do rio. A Figura 1.1.1 apresenta a regra que cria o operador e a regra que defini a estrutura de representação do estado.

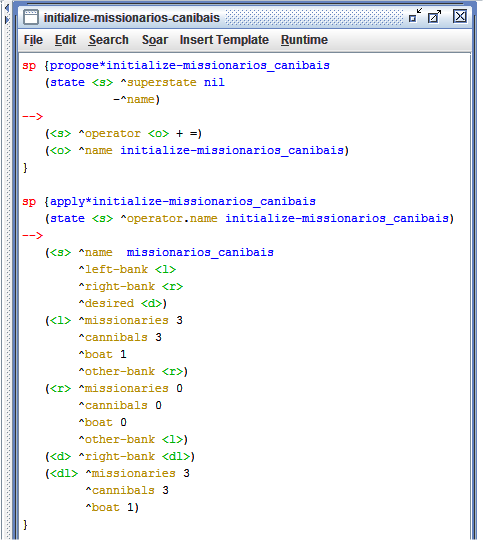
Figura 1.1: Representação do estado.

Os operadores do problema Missionários e Canibais devem mover 1 ou 2 pessoas no barco de uma margem para outra do rio. Para realizar essa operação, pode-se criar três opções de classes:

• Mover um missionário ou um canibal para a outra margem.
• Mover dois missionários ou dois canibais para a outra margem.
• Mover um missionário e um canibal para a outra margem.

As classes da operação de mover canibais e missionários para a outra margem podem ser representadas pelas regras mostradas na Figura 1.2.

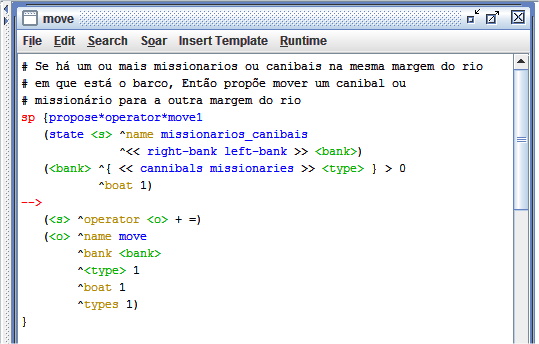
Figura 1.2: Operador move.

As regras apresentadas na Figura acima, são generalizadas para o lado da margem, ou seja, a mesma regra se aplica para a margem direita ou esquerda, pois na definição da margem está sendo usada a variável bank. As regras também são generalizadas para o tipo de pessoa (missionário ou canibal). Além disso, na regras apresentadas acima, o valor do argumento types representa a quantidade de pessoas de diferentes tipos está sendo carregada no barco. Logo, se estão sendo transportados só canibais ou só missionários, o valor desse argumento é um, mas, se está sendo transportado um canibal e um missionário ao mesmo tempo, o valor desse argumento é 2. Outro ponto importante é que as regras apresentadas na Figura 1.2 possuem preferência aceitável e indiferente.

Após criar as regras que propõem o operador move, é necessário criar a regra de aplicação desse operador. Essa regra deve mudar o estado e representar o movimento do barco, dos missionários e dos canibais em relação às margens do rio. Para isso, basta diminuir o número de missionários e canibais na margem em que está o barco e aumentar o número desses indivíduos na margem de destino do barco. A Figura 1.3 apresenta a regra de aplicação do operador move.

Figura 1.3: Regra de aplicação do operador move.

Conforme pode ser observado na Figura 1.3, a regra de aplicação do operador move é generalizada para os três tipos de objetos: barco, missionário e canibal. Para promover essa generalização foi usada a variável type. Para complementar, também foi usada a variável number, que representa o número de objetos que estão sendo movidos de uma margem para outra do rio.

A variável bank-num da regra de aplicação do operador move é usada para representar o número de objetos de um determinado tipo que estão na margem atual. Já a variável obank-num é usada para representar o número de objetos de um determinado tipo que estão na margem oposta à margem atual. Portanto, a penúltima ação da regra apresentada na Figura 1.3 está diminuindo o número de objetos de um determinado tipo na margem atual, enquanto que a segunda ação está aumentando o número de objetos de um determinado tipo para a margem oposta à margem atual.

Depois de desenvolver a regra de aplicação do operador move, foram criadas as regras de monitoramento apresentadas na Figura 1.4. A primeira regra imprime o tipo de objeto (missionários e canibais) que será transpostado no rio de uma margem para outra e o número de objetos de um determinado tipo. Por outro lado, a segunda e terceira regra imprimem, respectivamente as informações referentes à margem esquerda e direita, que incluem o número de canibais, número de missionários e em qual margem se encontra o barco.

Figura 1.4: Regra de monitoramento.

Veja na Figura 1.5 o resultado das regras de monitoramento ao executar o programa no Soar Debugger.

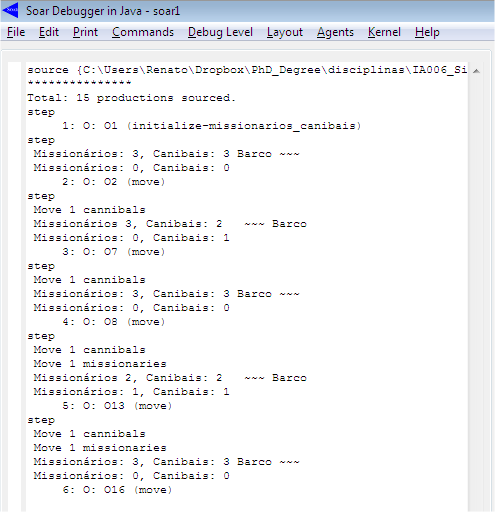
Figura 1.5: Regra de monitoramento no Soar Debugger.

Conforme pode ser visto na Figura 1.5, o programa está funcionando. Porém, ele é executado infinitamente, pois ele não sabe quando tem que parar, ou seja, quando o objetivo do problema é atingido. Assumiu-se que a solução do problema é ter o mesmo número de missionários e canibais na mesma margem do rio. Diante disso, foi criada uma regra que para a execução do programa quando o problema Missionários e Canibais é resolvido, conforme pode ser visto na Figura 1.6.

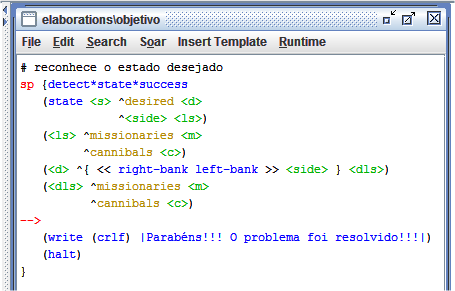
Figura 1.6: Regra que reconhece o estado desejado.

Outro ponto importante também, é identificar quando o problema falha, ou seja, quando em alguma margem do rio, o número de canibais supera o número de missionários e o número de missionários nessa margem é maior do que zero. Se isso acontecer, os canibais se alimentam dos missionários e por isso, a solução do problema fracassa. Diante disso, na Figura 1.7, é apresentada a regra que foi criada para identificar essa situação.

Figura 1.7: Regra que reconhece o estado de falha.

Com as regras implementadas até o momento, quando um estado de falha é atingido, o programa para. Porém uma das formas de evitar que o programa pare sem encontrar a solução desejada, é voltar um passo atrás e procurar outra solução. Para isso, deve-se criar uma estrutura na memória de trabalho que armazene a última ação. Então, é necessário criar uma regra para quando um único tipo de objeto é transportado de uma margem para outra do rio e outra para quando um missionário e um canibal são transportados ao mesmo tempo.

A estrutura criada para armazenar a última ação foi chamada de last-operator. Essa estrutura precisa ser removida da memória de trabalho quando for observado que a margem armazenada nela, é diferente da margem em que o barco está atualmente. Veja na Figura 1.8 as regras para armazenar e remover a estrutura da memória de trabalho que guarda a última ação do agente.

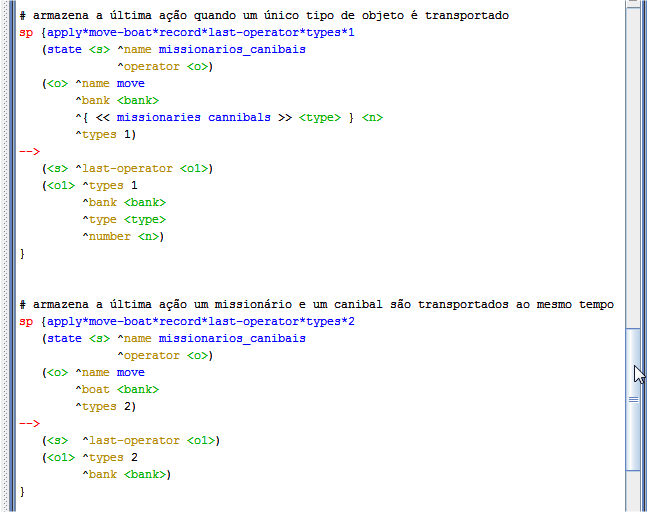
Figura 1.8: Regras que armazenam e removem da memória de trabalho a estrutura que guarda a última ação do agente.

Para as regras apresentadas na Figura 1.8 serem executadas, é necessário alterar a regra que detecta que foi obtido um estado de falha (Figura 1.7). Da maneira como está até o momento, ao encontrar o estado falho o programa para de executar. As únicas alterações necessárias são retirar a ação que faz o programa parar e retirar a ação com o comando write que informa ao usuário que o programa falhou, além de acrescentar um argumento que identifica que foi encontrado um estado de falha, conforme é apresentado na Figura 1.9.

Figura 1.9: Atualização da regra que reconhece o estado de falha.

O próximo passo é criar regras que deem preferência para os operadores que voltam para a última ação quanto o estado de falha é encontrado. Da mesma forma que nas regras apresentadas na Figura 1.8, deve ser criada uma regra para quando um único tipo de objeto é transportado de uma margem para outra do rio e outra para quando um missionário e um canibal são transportados ao mesmo tempo. Veja, na Figura 1.10, as regras que foram criadas para esse propósito.

Figura 1.10: Regras que criam preferência para os operadores que voltam para a última ação quanto o estado de falha é encontrado.

Um problema criado pelas regras apresentadas na Figura 1.10 é que elas podem desfazer o operador quando o último estado não foi um estado de falha. Isso pode acontecer porque o inverso do operador pode ser selecionado pelo Soar. Então, para evitar isso, as regras mostradas na Figura 1.11 foram criadas para evitar que a última ação seja desfeita quando um estado de falha não foi encontrado.

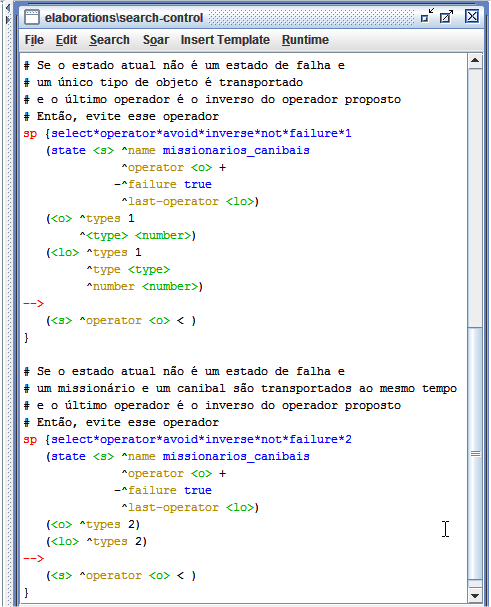
Figura 1.11: Regras que evitam que a última ação seja desfeita quando um estado de falha não foi encontrado.

Com as regras apresentadas nesse exercício, o programa funciona perfeitamente, encontrando a solução desejada, conforme pode ser visto na Figura 1.12, que apresenta parte da execução do programa no Soar Debugger.

Figura 1.11: Execução do programa no Soar Debugger.

Exercício 2

Nesse exercício foram feitas modificações nos programas Missionários e Canibais e Water Jug de forma que eles usem subobjetivos para planejar e aprender. O planejamento que será apresentado nesse exercício é do tipo "olhar para frente" look , que é o mais natural do Soar. Ao usar esse tipo de planejamento, o programa experimenta os operadores internamente para avaliá-los, antes de aplicá-los na tarefa real. O tipo de aprendizagem que usa planejamento e subobjetivos é chamado de chunking, que é uma forma de generalização baseada em explicação.

O problema Water Jug (jarro d'água)

O planejamento no Soar involve a detecção de impasses e mecanismos de criação de subestados. Então, o primeira passo para a criação de planejamento é eliminar as preferências indiferentes das regras de proposição dos operadores. Então, considerando o operador fill do problema Water Jug, ao eliminar a preferência indiferente da regra que o propõe, obtém-se a regra apresentada na Figura 2.1.1.

Figura 2.1.1: Operador fill sem preferência indiferente.

Sem a preferência indiferente, ao executar o programa é obtido um tie impasse e o Soar gera novos substados, pois as preferências são insuficientes para escolher algum operador. Quando esse fenômeno ocorre, o operador tem os seguintes argumentos: ^choices multiple, ^impasse tie, e ^item para cada operador empatado. Observe a execução do programa Water Jug no Soar Debugger e as características que indicam que houve um tie impasse.

Figura 2.1.2: Tie impasse no operador fill .

Quando ocorre um tie impasse, o objetivo é determinar qual tarefa do operador é mais apropriada para se aplicar no estado atual. Esse objetivo pode ser atingido por seleção e aplicação de operadores de avaliação nos subestados, para cada tarefa do operador. Esses operadores tem o objetivo de avaliar as tarefas do operador fornecendo algum medida de desempenho, tais como fracasso, sucesso ou um valor numérico da probabilidade de sucesso. Essas medidas podem ser convertidas em preferências para as tarefas do operador. Com esse mecanismo, se, por exemplo, um operador é avaliado e verifica-se que ele leva diretamente para o objetivo, então pode-se definir uma melhor preferência a esse operador, o que pode ser suficiente para resolver um impasse.

O problema de resolver um tie impasse é chamado de problema de Seleção (Selection problem). Para resolver o problema de Seleção deve-se criar regras e operadores como em qualquer outro problema do Soar. Porém, embora alguns problemas possam necessitar de regras específicas, normalmente a solução do problema de Seleção é generalizada e necessita de apenas algumas modificações específicas para um determinado problema. O Soar já fornece regras genéricas para o problema de Seleção, que podem ser encontradas no seguinte diretório, a partir da pasta raíz do Soar: Agents/default/selection.soar. A Figura 2.1.3 apresenta a estrutura do programa selection.soar no Visual Soar.

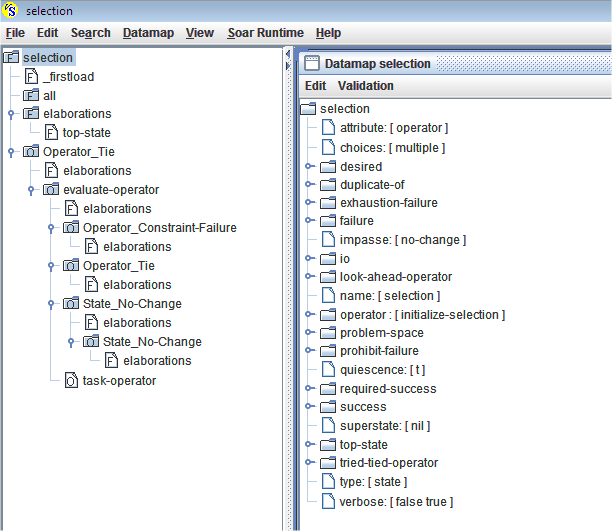
Figura 2.1.3: Estrutura do programa selection.soar no Visual Soar.

Para usar as regras do programa selection.soar no problema Water Jug, basta adicionar o seguinte comando nos arquivos Soar do problema:

 pushd ../default
 source selection.soar
 popd
	

Na primeira linha do comando apresentado acima, considera-se que o programa esteja em um subdiretório do diretório Agents. Caso não esteja, deve-se alterar para o caminho correto em relação ao diretório em que o programa Soar está inserido.

O primeiro passo para a solução do problema de Seleção é a definição da estrutura de representação do estado do problema, que é chamado de selection. Para esse problema, os operadores devem criar e comparar avaliações. Essas avaliações possuem um valor chamado evaluation que têm os seguintes argumentos:

• ^operator <o>: identifica o operador da tarefa que está sendo avaliada;
• symbolic-value success/partial-success/partial-failure/failure/indifferent;
• numeric-value [number];
• value true: indica que há um valor simbólico ou numérico;
• desired <d>: identifica o estado desejado;

Depois de criar a estrutura de representação do estado, normalmente cria-se as regras que geram o estado inicial. Porém, no problema de Seleção, o estado é automaticamente criado em resposta a um impasse. A única regra que é necessária é a que nomeia o estado. Ela não é obrigatória, mas dar um nome para o estado facilita testar o nome do estado em regras posteriores. Veja a regra sugerida na Figura 2.1.3.

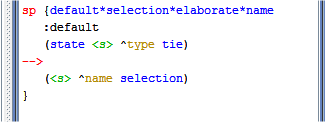
Figura 2.1.4: Regra que nomeia o estado.

Conforme pode ser observado na regra apresentada pela Figura 2.1.2, uma nova sintaxe é usada: default. Isso indica para o Soar que a regra é padrão. Apesar desse tipo de regra não se comportar diferente de outras regras, o soar mantém estatísticas diferentes para ela e permite que regras não-padrão possam ser excluídas facilmente. Todas as regras nomeadas como default estão incluídas no arquivo selection.soar que se encontra no seguinte diretório, a partir da pasta raíz do Soar: Agents/default/selection.soar.

Após criar a regra que nomeia o estado do problema de Seleção, foi criado o único operador do problema: o evaluate-operator. Este operador deve ser proposto se existir algum item que não tem nenhuma avaliação com um valor. Nesse caso, primeiramente o operador cria uma avaliação e depois calcula o valor.

Figura 2.1.5: Regra que propõe o operador evaluate-operator.

Quando o operador evaluate-operator é selecionado, ele permanece selecionado até que uma avaliação adequada é criada com um valor. Por isso, apenas um operador evaluate-operator é criado e aplicado para cada tarefa do operador que esteja empatada.

O próximo passo na solução do problema de Seleção é a aplicação do operador proposto na regra apresentada na Figura 2.1.4. A aplicação desse operador é dividida em duas partes. A primeira é a criação da estrutura de avaliação dos dados. Essa estrutura é fornecida no arquivo selection.soar e é formada pelos seguintes argumentos:

	
(<s> ^evaluation <e>
     ^operator <o>)
(<e> ^superoperator <so>
     ^desired <d>)
(<o> ^name evaluate-operator
     ^superoperator <so>
     ^evaluation <e>
     ^superstate <ss>
     ^superproblem-space <sp>)

Na estrutura apresentada acima, o argumento desired é um objeto que descreve o estado desejado para o problema que está sendo resolvido. Então, o operador recebe uma avaliação proporcional ao quanto ele contribui para ajudar a atingir esse estado. Por outro lado, o argumento superproblem-space é o objeto que representa o espaço do problema no superstate, ou seja, é uma representação sobre o estado das propriedades do espaço do problema atual. .

A segunda parte da aplicação do operador proposto na regra apresentada na Figura 2.1.4 é o calculo da avaliação, que não pode ser realizado diretamente nas regras, mas requer seu próprio subestado, que é chamado de problema evaluation. A tarefa original é copiada para esse subestado e o operador dessa tarefa é aplicado para o estado. Caso o novo estado possa ser avaliado, então o valor dessa avaliação é retornado e adicionado na propriedade do objeto evaluation. Porém, se o novo estado não puder ser avaliado, então a solução do problema continua até que uma avaliação possa ser feita.

Diante do que foi apresentado até o momento, pode-se observar que é necessário ter cuidado na criação das regras de um problema no Soar, quando deseja-se usar o planejamento do tipo "olhar para frente". Por exemplo, a regra de aplicação do operador fill do problema Water Jug precisa ser modificada para usar esse tipo de planejamento, pois ela modifica os argumentos content e empty do objeto jug diretamente no estado original. Para usar o planejamento do tipo "olhar para frente" é necessário modificar a cópia dos argumentos e não o estado original. Então, para solucionar esse problema a solução recomendada é copiar dois níveis de atributos, adicionando as seguintes ações na regra de inicialização do estado original do problema Water Jug.

Figura 2.1.6: Regra de elaboração do estado necessário para o uso do planejamento do tipo "olhar para frente".

Depois que o estado inicial do operador evaluate-operator é criado, a cópia dos operadores que estão sendo avaliados precisam ser selecionadas. Então, automaticamente é feita a duplicação do operador e a substituição dos identificadores na estrutura do operador que foram alteradas nesse processo de duplicação. Por exemplo, no problema Water Jug, o identificador j1 é substituído pelo identificador j3. Diante disso, todos os operadores propostos são rejeitados de forma que a cópia seja sempre selecionada. Após selecionar a cópia, as regras de aplicação modificam o estado copiado.

Com a criação de um novo estado, uma avaliação pode ser feita. Para isso, um argumento ^tried-tied-operator é adicionado em paralelo ao operador que está sendo aplicado. Ele pode ser testado por regras para garantir que a avaliação está sendo feita em relação ao resultado da aplicação do operador e não da cópia do estado original. Uma simples forma de avaliação é determinar se a solução teve sucesso (atingiu o objetivo) ou fracasso (não atingiu o objetivo). Essa forma de avaliação foi criada para o problema Water Jug, usando a regra apresentada na Figura 2.1.7.

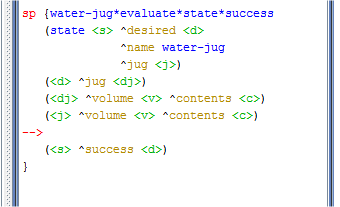
Figura 2.1.7: Avaliação do tipo sucesso ou fracasso.

Ao adicionar as regras apresentadas nas Figuras 2.1.6 e 2.1.7, pode-se afirmar que o programa que tenta solucionar o problema Water Jug está usando o planejamento do tipo "olhar para frente". A Figura 2.1.8 mostra parte da execução do programa Water Jug com as regras que aplicam o planejamento do tipo "olhar para frente".

Figura 2.1.8: Programa Water Jug usando o planejamento do tipo "olhar para frente".

Diante do que é apresentado na Figura 2.1.8, percebe-se há um problema, pois a cada operador selecionado é criado um tie impasse e uma pilha recursiva de subestados que tentam resolver o tie impasse. Quando uma solução é encontrada, ela é aplicada para selecionar apenas o operador relacionado ao tie impasse mais recente. Diante disso, é necessário redescobrir a solução quando ocorre um novo tie impasse. Outro problema é que o sistema, muitas vezes, revisita o mesmo estado e gera um tie impasse idêntico ao último nível da pilha de estados.

Para resolver o segundo problema foi criado uma regra que avalia os estados que apresentaram falha, ou seja, os estados que foram duplicados por um estado anterior que já está na pilha de estados. Essa regra deve testar o estado desejado, o conteúdo do estado e qual estado existe depois que o operador é aplicado em uma avaliação. Além disso, a regra precisa testar se o estado foi duplicado em uma pilha de estados anterior. Para isso, é necessário criar regras de elaboração de cada estado com todos os seus superestados, formando o que é chamado de conjunto de superestados (superstate-set). A regra que foi criada para adicionar o superestado para o conjunto de superestados e a regra que adiciona todos os conjuntos de superestados do estado para seu superestado, são apresentadas na Figura 2.1.9. Já, a regra que foi criada para resolver o problema dos estados com falha é apresentada na Figura 2.1.10.

Figura 2.1.9: Regra que adiciona o superestado para o conjunto de superestados e regra que adiciona todos os conjuntos de superestados do estado para seu superestado.

Figura 2.1.10: Regra que detecta estados que apresentaram falha.

Para resolver o primeiro problema, em que um tie impasse está sendo criado cada vez que um operador é selecionado, foi usado o mecanismo de chunking. Esse mecanismo examina os elementos da memória de trabalho que são criados por regras adicionadas quando um resultado é produzido em um subestado. Caso algum desses elementos possua alguma ligação com algum superestado, ele torna-se condição da nova regra. Isso evita que um tie impasse ocorra novamente para um operador que já tenha sido selecionado, pois agora, ele passa a ser tratado como uma condição da nova regra.

Para invocar o mecanismo de chunking basta adicionar o comando learn –-on no prompt do Soar Debugger ou adicioná-lo no arquivo que contém as regras do programa que usará esse mecanismo para melhorar seu funcionamento. Para monitorar quando os chunks são criados e monitorados, pode-se usar o comando watch --chunks. Com isso, ao executar o programa Water Jug no Soar Debugger, observa-se que a resolução do problema é muito mais rápida e eficiente. A Figura 2.1.11 mostra parte da execução do programa.

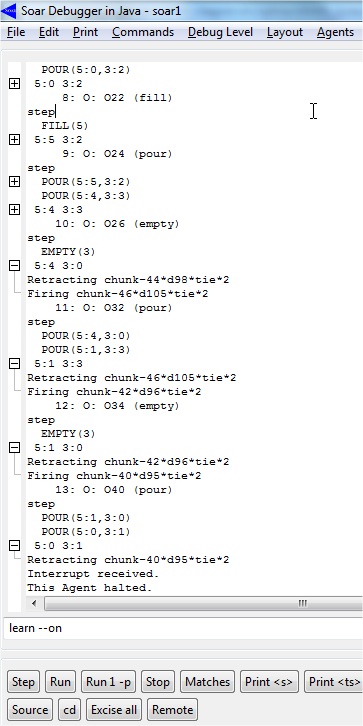
Figura 2.1.10: Programa Water Jug atualizado.

O problema Missionários e Canibais

As etapas apresentadas na seção anterior, para aplicar o planejamento do tipo "olhar para frente" com o objetivo de melhorar a solução do problema Water Jug, também foram seguidas para aplicar esse tipo de planejamento no programa que tenta solucionar o problema Missionários e Canibais.

Tal como foi feito na seção anterior, para usar o planejamento do tipo "olhar para frente", foram adicionados, no programa Missionários e Canibais, os comandos que importam as regras do programa selection.soar. Depois disso, foi adicionada a regra que defini o espaço do problema e especifica como a cópia dos argumentos do estado será feita para a avaliação. Na seção anterior, essa regra foi apresentada na Figura 2.1.6. Nessa seção ela foi modificada e incluída no programa Missionários e Canibais, conforme é apresentado na Figura 2.2.1.

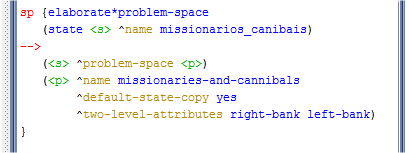
Figura 2.2.1: Regra de elaboração do estado necessário para o uso do planejamento do tipo "olhar para frente"..

O próximo foi a alteração da regra que faz o programa parar quando o estado desejado é obtido. Com a alteração apresentada na Figura 2.2.2, em vez do programa parar, ele recebe uma avaliação que indica que ele obteve sucesso.

Figura 2.2.2: Avaliação do programa quando ele atingi o estado desejado..

Também foi modificada a regra que identifica quando o programa falha, ou seja, quando em alguma margem do rio, o número de canibais supera o número de missionários e o número de missionários nessa margem é maior do que zero. Com a alteração apresentada na Figura 2.2.3, em vez do programa parar, ele recebe uma avaliação que indica que fracassou na solução do problema.

Figura 2.2.3: Avaliação do programa quando ele fracassa na solução do problema Missionários e Canibais..

Também foi modificada a regra que identifica quando o programa falha, ou seja, quando em alguma margem do rio, o número de canibais supera o número de missionários e o número de missionários nessa margem é maior do que zero. Com a alteração apresentada na Figura 2.2.3, em vez do programa parar, ele recebe uma avaliação que indica que fracassou na solução do problema.

Com essas alterações pode-se dizer que o programa já está usando planejamento. Porém, há problemas tal como ocorreu com o programa Water Jug, pois a cada operador selecionado é criado um tie impasse e o sistema, muitas vezes, revisita o mesmo estado e gera um tie impasse idêntico ao último nível da pilha de estados. Esses problemas podem ser observados pelo execução do programa no Soar Debugger, conforme mostra a Figura 2.2.4.

Figura 2.2.5: Programa Missionários e Canibais usando o planejamento do tipo "olhar para frente"..

Para resolver um dos problemas mencionados, a regra mostrada na Figura 2.2.5, foi criada com o objetivo de detectar estados duplicados na pilha de estados e avaliar o mais recente como estado de falha.

Figura 2.2.5: Regra que detecta estados duplicados na pilha de estados e avalia o mais recente como estado de falha...

Para aumentar a eficiência do programa Missionários e Canibais e resolver o primeiro problema, em que um tie impasse é criado cada vez que um operador é selecionado, foi usado o mecanismo de chunking. Com esse mecanismo os problemas mencionados foram resolvidos e a solução foi encontrada com maior rapidez. A Figura 2.1.11 mostra parte da execução do programa.

Figura 2.2.6: Execução do programa Missionários e Canibais usando o mecanismo de chunking.

Apesar do mecanismo de chunking ter melhorado o desempenho do programa na solução do problema Missionários e Canibais, ele pode ser melhorado ainda mais coma adição de uma função de avaliação que dê preferência a um estado que tenha mais missionários e canibais para levar para a outra margem do rio. Para que isso seja possível, a regra que defini a estrutura de representação do estado (Figura 1.1) foi alterada, adicionando-se um valor para o argumento desired, que avalia o estado com maior número de missionários e canibais como ^better higher, que poderia ser traduzido como "quanto mais melhor". Veja a regra atualizada na Figura 2.2.7.

Figura 2.2.7: Atualização da regra que defini a estrutura de representação do estado.

Para que o argumento adicionado na regra da figura acima ajude a selecionar o estado com maior número de missionários e canibais, foi criada uma regra que avalia o estado. Quanto mais missionários e canibais o estado tiver, melhor será sua avaliação. O valor retornado por essa regra é numérico, conforme pode ser visto na Figura 2.2.8.

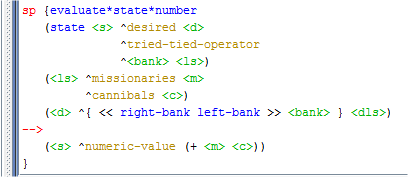
Figura 2.2.8: Regra que avalia o estado.

Usando a regra apresentada na figura acima, o programa consegue resolver o problema Missionários e Canibais mais rápido, pois ao dar preferência aos operadores que carregam mais canibais e missionários, mais rápido todos eles são transportados para a outra margem do rio.