You are here

Home » 2015-9

b) Aula 2 - SOAR: Tutorial 1

published by 2015-9 on Fri, 03/13/2015 - 19:02

Relatório 2 - SOAR - Tutorial 1.

 

Conteúdo:

Atividade 1: Instalando o SOAR.

  -Download:

 

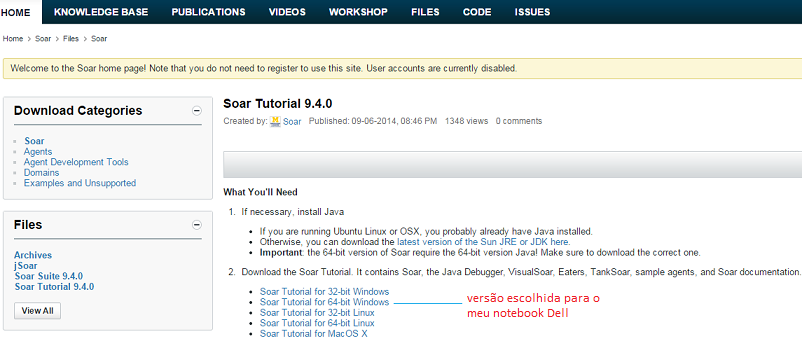
  - Diretório do SOAR:

 

Atividade 2: Construindo um Agente SOAR Simples usando Regras.

    Criando um Agente SOAR e Utilizando o SOAR Debugger:

     # Executando o Hello World do SOAR

O objetivo desta atividade, como todo programa Hello World, é apresentar as funcionalidades básicas da plataforma/arquitetura. Portanto, será criado um agente simples para o entendimento. O roteiro recomenda utilizar o SOAR Debugger, já que este permite depurar a execução do programa e trackear passo a passo o seu funcionamento. Para executar o SOAR Debugger, execute o arquivo SoarJavaDebugger.sh, que se encontra na raiz da pasta onde foi instalado o SOAR. Tela inicial do SOAR Debugger:

 

Após carregado, o programa HelloWorld é executado:

 

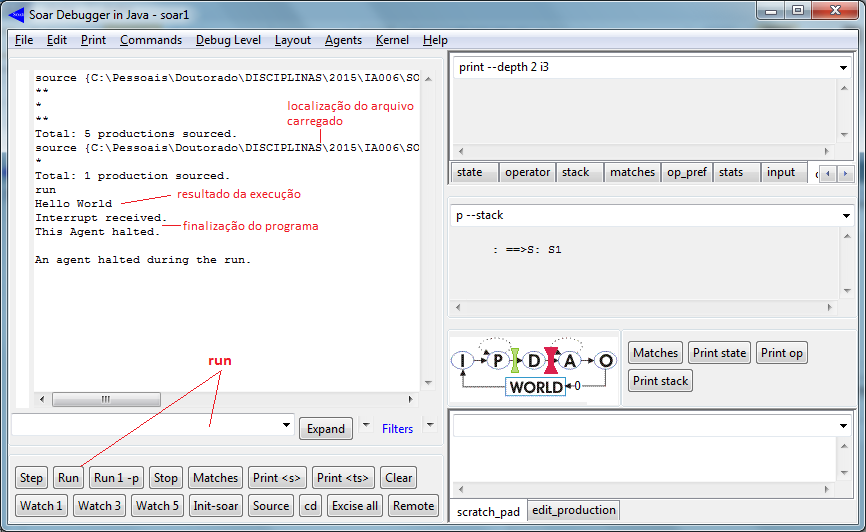
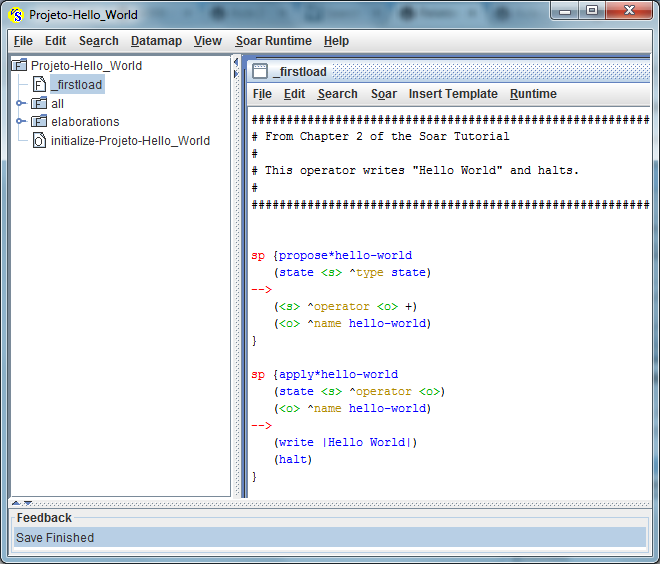
O código deste programa SOAR é bastante simples e pode ser visualizado no VisualSoar:

 

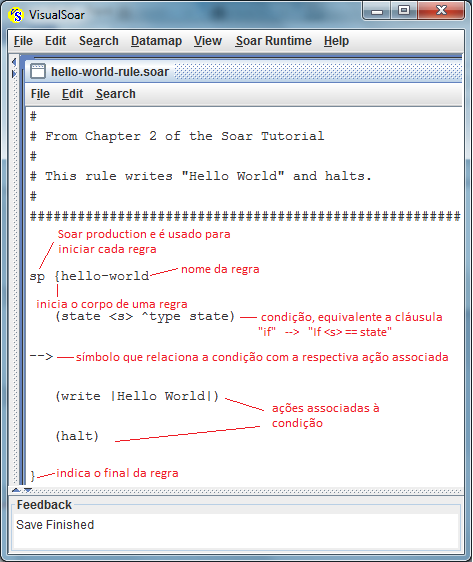
Toda regra SOAR segue o seguinte "template":

 

      Utilizando a Memória de Trabalho

De forma simplificada, o processamento na arquitetura SOAR consiste da combinação apropriada e disparo de regras. As regras proporcionam uma representação do conhecimento flexível e, ao mesmo tempo, dependente do contexto, com suas ações dependendo da combinação de suas condições com as informações descritas na situação atual (contexto da working memory). Na arquitetura SOAR, existem regras que propõe operadores que criam novas estruturas de dados na memoria de trabalho, representando o operador e sua preferência, de forma que o operador possa ser considerado na seleção de ações. Existem também regras que avaliam os operadores e criam outros tipos de preferências capazes de de estabelecer indicações de preferencias entre os operadores disponíveis para a situação atual. Um trerceiro tipo de regra é aquela responsável pela aplicação da regra, mudando a memória de trabalho e refletindo as ações do operador sobre a situação atual.

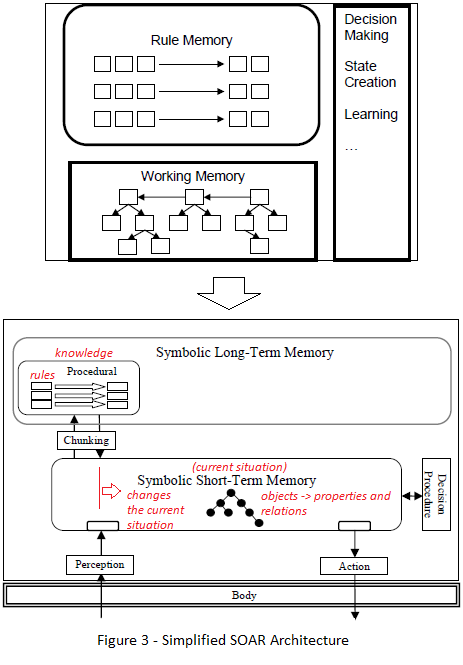
De forma a dar suporte à seleção e aplicação de operadores e proporcionar a interface para ambientes externos, Soar apresenta ciclo de processamento mostrado na Figura 4.

1. Entrada. Alterações à percepção são processados e enviados para a memória de curto prazo.

2. Elaboração. Regras avaliam vinculações de memória de curto prazo e a situação corrente. Por exemplo, uma regra pode testar se o objetivo é agarrar um objeto, a distância do objeto, e alcance do agente. Em seguida, cria uma estrutura de dado descrendo se o objeto está ao alcance e detalhes relevantes.

3. Proposta de Operador. Regras propõe operadores apropriados à situação atual, com base nas características da situação testada e nas condições das regras.

4. Avaliação do Operador. Regras criam preferências para os operadores propostos, com base na situação atual e no objetivo. As preferências podem ser simbólicas (A é melhor do que B), ou numéricas (a utilidade estimada de A é 0,73).

5. Seleção de Operador. O procedimento de decisão combina e avalia as preferências geradas e seleciona o operador. Se as preferências são insuficientes para tomar uma decisão, um impasse surge e o SOAR cria automaticamente um subestado cujo objetivo é resolver este impasse. No subestado, SOAR utiliza o mesmo ciclo de processamento, selecionando e aplicando operadores, de forma recursiva levando à solução automática e reativa, como um “meta-raciocínio”. Os impasses e subestados resultantes fornecem um mecanismo para executar deliberadamente qualquer uma das funções (elaboração, proposta, avaliação e aplicação) que são executadas automaticamente/reativamente através das regras.

6. Aplicação do Operador. As ações do operador são realizadas por regras que correspondem a situação atual e a estrutura operador. Várias regras pode disparar em paralelo e em seqüência, fornecendo um meio flexível e expressivos para ações do operadores. Se houver conhecimento insuficiente para a aplicação do operador, um impasse surge e leva à criação de um substado. Isto leva à decomposição dinâmica tarefas, onde um operador complexo é executado de forma recursiva por operadores mais simples.

7. Saída. Todos os comandos de saída são repassados para o sistema motor (engine).

A memória de trabalho contém todas as informações dinâmicas de um agente Soar, sobre o seu mundo e seu raciocínio interno. Ela contém sensores, cálculos intermediários, operadores e objetivos. Em Soar, toda a memória de trabalho está organizado como grafos de estados. Assim, cada elemento da memória de trabalho está conectado, direta ou indiretamente, a um símbolo de estado. Abaixo está um exemplo simples do que a estrutura da memória de trabalho pode ser, no caso em que o agente representa a existência de dois blocos, um em cima do outro, sobre uma mesa, como mostrado na figura abaixo:

 

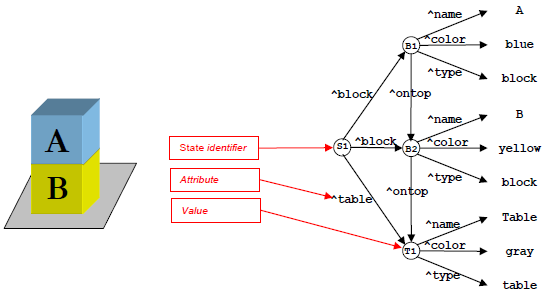
A figura do grafo abaixo ilustra uma estrutura básica de memória de trabalho criada automaticamente pelo SOAR para todos os agentes. Portanto, apesar de não ser normalmente mostrado, o estado inicial S1 apresenta a seguinte estrutura:

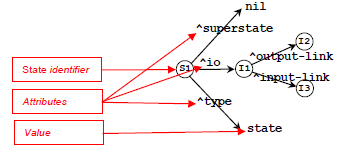
Como um gráfico, há nós (ou vértices) e links (ou arestas). Os nós, tais como S1, B1, B2, A, e “blue”, estão conectados por links, como block, table, name, color e supertate. Soar tem dois tipos de nós: identificadores e constantes. Os nós que podem ter ligações que deles emana, nós não terminais, como S1 e B1, são chamados identificadores, enquanto os outros, nós terminais, como state, blue, block, e nil, são chamados constantes.
No exemplo acima, S1 é o identificador para o estado. Todos os símbolos identificadores são criados automaticamente por Soar e constituído por uma única letra seguida por um número. Embora I2 e I3 na figura mais a baixo não tem quaisquer ligações que emanam deles, eles são identificadores e podem ter
subestruturas adicionadas. Em contraste, o símbolo state não é um identificador e não pode ter links que emanam a partir dele. Os links são chamados atributos em Soar e são precedidos por um "^". Somente identificadores têm atributos. Na figura de fundo, S1 tem três atributos: superstate, io, e type. I1 tem dois: output-link e input-link

 

Atividade 3: Agentes Simples utilizando Operadores.

O programa "Hello-World" desenvolvido anteriormente apresentava apenas uma regra, de aplicação direta, sem operadores. Isto faz algum sentido já que trata-se de uma única regra no contexto e de aplicação realmente direta. 

Obviamente, o mais comum é termos contextos mais complexos, onde regras terão suas condições avaliadas e comparadas aos estados existentes na memória de trabalho, e os operadores recomendados por estas regras aplicados ao contexto, modificando a situação corrente. Para usar um operador, é necessário duas regras: uma para propor o operador e outra para aplicá-lo quando ele é selecionado.

A tela do VisualSOAR mostra o programa "Hello-World" modificado para conter regras que recomendam um operador em caso de uma situação específica.

 

 

 

O Tutorial faz algumas recomendações de configuração do SOARdebugger antes da execução:

- Usar o comando excise –all, ou o botão correspondente, para destruir agentes executados anteriormente e limpar todas as regras existentes na memória.

- Alterar o nível watch para watch 5, fazendo com que o Soar Debugger apresente mais detalhes da execução. 

A execução no SOAR Debugger:

 

     Utilizando o Visual SOAR:

 

Um dos recursos mais importantes do Visual SOAR é o Datamap. Esta ferramenta permite visualizar a estrutura de dados corrente na memória de trabalho:

 

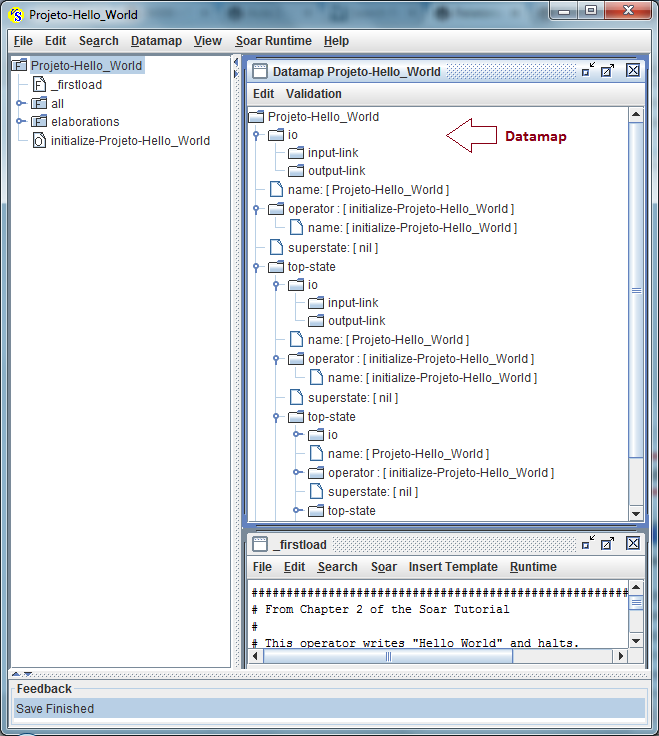
Áreas funcionais do IDE Visual SOAR:

 

Atividade 4: Criando um Agente para o Water Jug Problem.

Descrição do problema:

Water Jug Problem Statement: You are given two empty jugs. One holds five gallons of water and the other holds three gallons. There is a well that has unlimited water that you can use to completely fill the jugs. You can also empty a jug or pour water from one jug to another. There are no marks for intermediate levels on the jugs. The goal is to fill the three-gallon jug with one gallon of water.

Goal: to fill the three-gallon jug with one gallon of water.

Space of possible states: determined by the objects that are available to be manipulated (the two jugs) and their possible values (0-5 gallons full). A problem is then defined as an initial state that the problem solver starts at, (in this case two empty jugs) and a set of desired states (any state where the three-gallon jug has one gallon of water). To represent the states in the water jug problem, we will have two values: the amount of water in the five gallon jug, and the amount of water in the three gallon jug. For example: 5:0,3:0 will represent that the 5 gallon container has 0 gallons of water, and the 3 gallon container has 0 gallons of water. Below is a trace of the optimal solution for the problem showing the states and the operators that are applied to each state.

(5:0,3:0) Fill 3 gallon jug
(5:0,3:3) Pour 3 gallon jug into 5 gallon jug
(5:3,3:0) Fill 3 gallon jug
(5:3,3:3) Pour 3 gallon jug into 5 gallon jug
(5:5,3:1)

Problem solving: consists of starting at the initial state, then searching for a desired state by applying operators, which transform one state into another. For the water jug problem, the operators are fill a jug, empty a jug, and pour from one jug to the other.

knowledge: "never emptying a jug immediately after it has been filled".

Desenvolvimento:

A more general approach would be to represent each jug as an object that had two attributes:
• The amount of water each jug currently holds (^contents).
• The amount of water each jug can hold (^volume). In this scheme, the initial state would look something like this.
 
(state <s> ^jug <j1> ^jug <j2>)
(<j1> ^volume 5 ^contents 0)
(<j2> ^volume 3 ^contents 0)
 
Using this representation, you can write one set of rules for manipulating both jugs.
Although this representation is sufficient for defining and solving the problem, as you will see later, the rules to propose operators can be simplified if you add an attribute for the amount of water that can be added to a jug to fill it (^empty). As you will see later, the value of this augmentation can be computed dynamically using state elaboration rules that test the volume and contents augmentations and subtract the volume from the contents. Thus, states will include the following structures:
 
• An object for each jug (^jug).
• The amount of water each jug can hold (^volume).
• The amount of water each jug currently holds (^contents).
• The amount of empty space available in each jug (^empty).
 
Although this representation is sufficient, one more working memory structure is extremely useful: a description of the task that is being attempted, in this case water-jug. By having some description of the task, the rules we create can be specific to that task and easily combined with rules from other tasks without interference.
• The task name (^name water-jug)
 
 
Step 1 - Initial State Creation: The initialize-water-jug Operator.
As with every operator, we must define two types of rules: one to propose the operator and one to apply the operator. This operator should be proposed only at the beginning, before any task is selected. Thus, the proposal should be:
 
English Version:
water-jug*propose*initialize-water-jug
If no task is selected,
then propose the initialize-water-jug operator.
 
Writing this rule in Soar is a challenge given what you know so far. How can you test that no task has been selected or that no jugs are defined? In Soar it is possible to test for the absence of working memory elements by preceding the attribute with “-“. Every rule in Soar must have at least one positive condition, so you still need to test that the state exists and in this case we use (^superstate nil).
 
Then, SOAR Version:
 
To apply the initialize-water-jug operator, we need another rule. The initialization application rule adds the name to the state and creates the jugs with contents of 0. The rule needs to add working memory elements for the initial values of the jugs and their attributes.
 
 
This rule does not include the creation of the ^empty attribute – it will be created by another rule that dynamically computes it based on the volume and contents.
O Visual SOAR constroi automaticamente a memória de trabalho correspondente ao operador.
Para visualizar, selecione Datamap:
 
 
 
Persistência dos elementos da Memória de Trabalho:
 
When the water-jug*apply*initialize-water-jug rule fires, all of the structures in its action are added to working memory. At this point, it would be desirable for the initialize-water-jug operator to be removed from working memory so that other operators can be selected. This is exactly what Soar does because the conditions of the proposal rule no longer match (the conditions testing for the absence of a task and the absence of the jug augmentation fail to match because those structures have been added to working memory). Once that rule retracts, the rule that applied the operator also no longer matches because the operator is no longer in working memory. However, we do not want the application rule to remove the structures it created when it no longer matches. If it did, the system would never be able to make any real progress – it would get in an infinite loop of proposing and applying an operator, retracting its results, and then proposing and applying the operator again.
 
Soar automatically classifies rules as to whether they are part of an operator application or not. A rule is an operator application rule if it tests the selected operator and modifies the state. The working memory elements created by such a rule persist and are said to have operator-support, or o-support because they are created as part of an operator. These working memory elements can be removed by other operator applications rules, or if they become disconnected from the state (because of the removal of other working memory elements).
 
For non-operator application rules, including rules that propose an operator, rules that compare operators, rules that elaborate operators, or rules that elaborate the state, the working memory elements created by the rules are removed from working memory if the rule no longer matches. These working memory elements are said to have instantiation-support or i-support – meaning they will persist only as long as the rule instantiation that created them still matches.
 
State Elaboration:
 
For the Water Jug problem, the state elaboration will compute the amount of empty space in a jug:
 
English version:
water-jug*elaborate*empty
If the state is named water-jug and a jug can hold volume v and currently has
contents c, then add that it has v – c available (empty) space.
 
SOAR version:
 
 
 
 
Para a solução completa, ainda temos que implementar mais três operadores: fill, empty and pour.
 
English Version:
water-jug*propose*fill
If the task is water-jug and there is a jug that is not full,
then propose filling that jug.
 
water-jug*propose*empty
If the task is water-jug and there is a jug that is not empty,
then propose emptying that jug.
 
water-jug*propose*pour
If the task is water-jug and there is a jug that is not full and the other jug is not empty,
then propose pouring water from the second jug into the first jug.
 
SOAR version:
 
 
 
 
 
 
Reconhecimento do Estado Desejado - Objetivo Alcançado:
The final step in creating a program that not only solves Water Jug, but knows that it solved it is generating a rule that recognizes when a desired state has been achieved - three-gallon jug has one gallon in it.
 
English version:
water-jug*detect*goal*achieved
If the task is water-jug and there is a jug with volume three and contents one,
write that the problem has been solved and halt.
 
 
SOAR version:
 
 
 
Controle de Seleção de Operadores (Busca):
In order to make the search more efficient; you need to add rules that prefer operators that have the best chance of leading to one of the desired states. There are few general heuristics that you can use in the water jug. At this development we will concentrate on avoiding undoing the last operator that was applied, such as emptying a jug right after it has been filled, filling a jug after it has been emptied, or pouring water from one jug into the other right after the opposite pouring has been done.
Then, in order to avoid to inverse the last operation just executed, you need to record the operation and verify, avoiding the invertions:
 
English version:
 
water-jug*apply*operator*record*last-operator*pour
If the task is water-jug and the pour operator is selected,
then create an augmentation of the state (last-operator) with the name of the operator and a copy of the augmentations augmentation.
 
water-jug*apply*operator*remove*old*last-operator*pour
If the task is water-jug and a pour operator is selected and last-operator does not have the same name and fill-jug,
then remove the last-operator.
 
Once these rules added, implement the rules that avoid applying an operator that undoes the previous operator:
 
water-jug*select*operator*avoid*inverse*fill
If the task is water-jug and the last operator is empty
then avoid a fill.
 
water-jug*select*operator*avoid*inverse*empty
If the task is water-jug and the last operator is fill
then avoid an empty.
 
water-jug*select*operator*avoid*inverse*pour
If the task is water-jug and the last operator is pour from one jug
then avoid a pour the opposite way.
 
Executando o programa no SOAR Debugger chegamos à solução, como demonstra a figura abaixo:
 
 
 
 

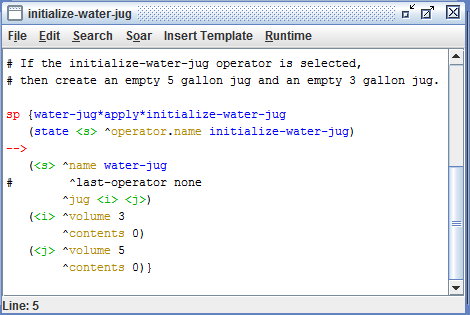
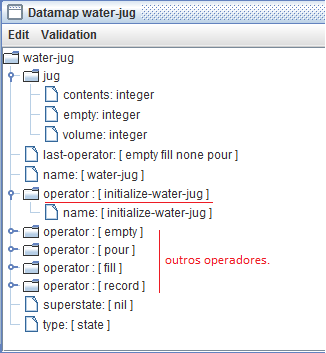
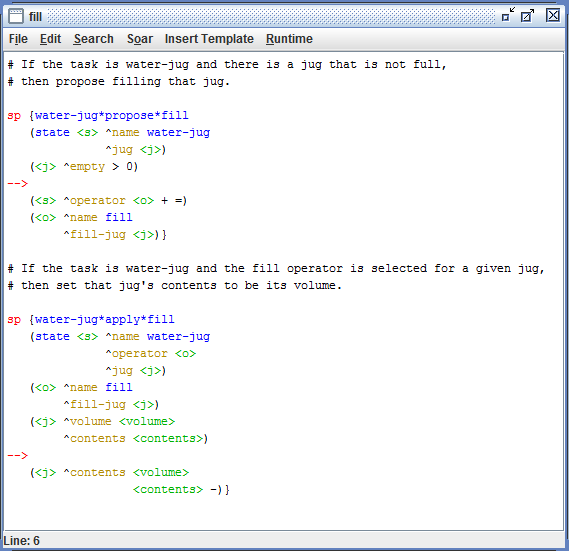
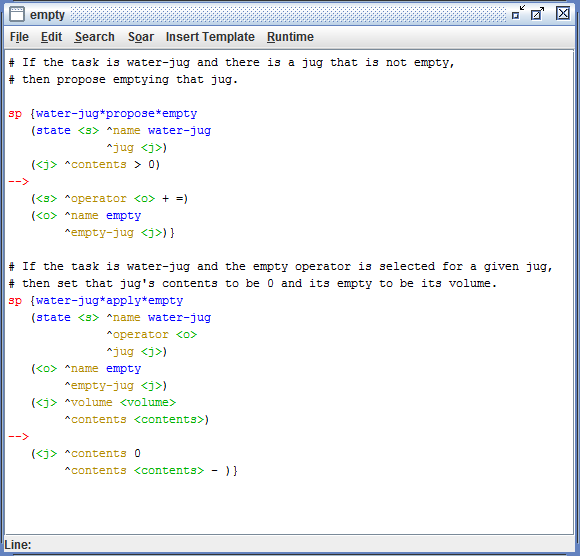
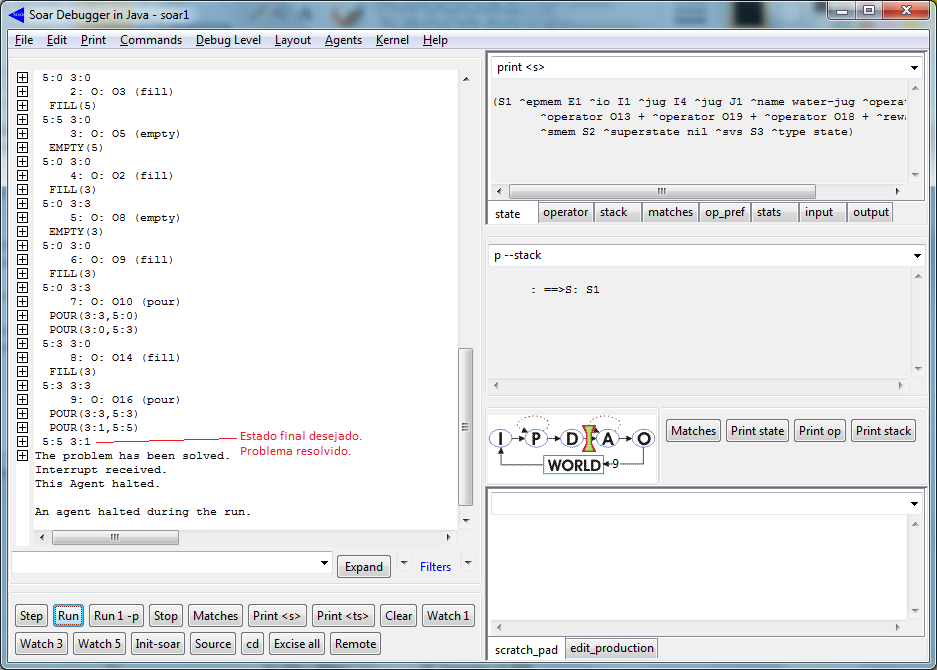
Observações e Conclusões:

Nesta aula foi possível entender melhor, na prática, os mecanismos da plataforma SOAR.

Foi possível perceber que a linguagem é bastante intuitiva, porém, caso a plataforma ganhe importância, ou seja empregada para a solução de problemas mais complexos, será necessário o desenvolvimento de uma linguagem de modelagem capaz de traduzir informações e mecanismos de “negócio” para a linguagem computacional.

Não parece ser uma tarefa impossível já que neste exercício vimos a semelhança entre as versões em inglês e em SOAR. Talvez um mapeamento UML -> SOAR seja possível.

De todos os artefatos e facilidades do SOAR que examinei neste exercício, o que mais me impressiona e chamou a atenção foi o papel das “Elaborations” descrito neste parágrafo:

“This rule will test the state and create a new structure on the state. This type of rule is called a state elaboration rule. State elaboration rules are ubiquitous in large Soar systems because they can create useful abstractions of combinations of other working memory elements and represent them directly on the state as a new augmentation. These new augmentations can then be tested in other rules in place of complex combinations of conditions, simplifying rules and making the structures in working memory more meaningful. A critical aspect of state elaboration rules is that they create i-supported working memory elements so that when the parts of the state they test change, they recompute their actions automatically.”

Tenho a impressão de que as “elaborations” tornam a plataforma SOAR mais interessantes e talvez seja por este artefato a viabilidade de integração com outros sistemas, permitindo melhorar o aspecto cognitivo e de inteligência. 

Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer