Aula 5 - Soar, Tutoriais 4 e 5

Tutorial 4 - Problema dos Missionários e Canibais

O tutorial 4 trata de um problema clássico em IA, que consiste em atravessar 3 missionários e 3 canibais de uma margem para a outra de um rio. Para isso é utilizado um barco para a travessia, que deve sempre ter 1 ou 2 pessoas. Além disso caso o número de canibais ultrapassar o de missionários em uma das margens em qualquer momento, chegamos em uma condição de fracasso na solução.

Seguindo a decomposição de um problema para sua implementação no SOAR, temos as seguintes etapas:

I. Representação dos estados.

Posições dos missionários, dos canibais, e do barco.

II. Regra da criação do estado inicial.

Todos os elementos na margem esquerda do rio.

III. Regras de proposição de operadores.

Propostas de mover 1 ou 2 missionários ou canibais junto com o barco.

IV. Regras de aplicação dos operadores.

Alterar os elementos da memória de trabalho do número de missionários/canibais em cada margem do rio, além da posição do barco.

V. Monitoramento de operadores selecionados e estados.

Monitora o número de elementos em cada margem e os operadores selecionados em cada etapa.

VI. Regra de reconhecimento de objetivo.

Todos os elementos na margem direita do rio.

VII. Regra de reconhecimento de fracasso.

Existem mais canibais do que missionários em alguma das margens.

VIII. Regras de controle de busca.

Deve-se desfazer o ultimo operador caso este leve a um estado de falha.

I. Representação dos estados.

Para o nosso problema não é necessário uma representação individual de cada missionário ou canibal, portanto podemos apenas representar o número de cada classe em cada margem. Assim os elementos a serem criados na memória de trabalho são:

1. Número de missionários em cada margem.

2.. Número de canibais em cada margem.

3. Número de "barcos" em cada margem (no caso será 1 na margem direita ou esquerda).

A representação em SOAR escolhida é a abaixo:

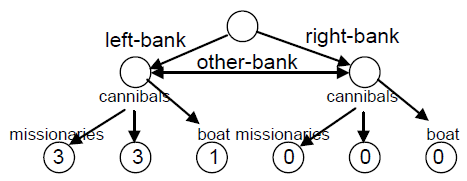
II. Regra da criação do estado inicial.

Aqui definimos que todos os elementos inicial na margem direita do rio:

sp {mac*propose*initialize-mac
   (state <s> ^superstate nil
             -^name)
-->
   (<s> ^operator <o> +)
   (<o> ^name initialize-mac)}

sp {mac*apply*initialize-mac
   (state <s> ^operator.name initialize-mac)
-->
   (<s> ^name mac
        ^left-bank <l>
        ^right-bank <r>
        ^desired <d>)
   (<r> ^missionaries 0
        ^cannibals 0
        ^boat 0
        ^other-bank <l>)
   (<l> ^missionaries 3
        ^cannibals 3
        ^boat 1
        ^other-bank <r>)
   (<d> ^right-bank <dr>)
   (<dr> ^missionaries 3
         ^cannibals 3
         ^boat 1)}

III. Regras de proposição de operadores.

Para este problema temos 3 propostas de regras:

1. Mover um missionário OU um canibal para o outro lado do rio, caso nesta margem exista ao menos um missionário ou canibal e o barco.

2. Mover dois missionários ou dois canibais para o outro lado do rio, caso nesta margem exista ao menos dois missionários ou dois canibais e o barco.

3. Mover um missionário E um canibal para o outro lado do rio, caso nesta margem exista ao menos um missionário e um canibal e o barco.

Proposição 1.

sp {mac*propose*move-mac-boat*1
   (state <s> ^name mac
              ^<< right-bank left-bank >> <bank>)
   (<bank> ^cannibals > 0
           ^boat 1)
-->
   (<s> ^operator <o> + =)
   (<o> ^name move-mac-boat
        ^bank <bank>
        ^boat 1
        ^cannibals 1
        ^types 1)}

Proposição 2.

sp {mac*propose*operator*move-mac-boat2
   (state <s> ^name mac
              ^ << right-bank left-bank >> <bank>)
   (<bank> ^{ << cannibals missionaries >> <type> } > 1
           ^boat 1)
-->
   (<s> ^operator <o> + =)
   (<o> ^name move-mac-boat
        ^bank <bank>
        ^<type> 2
        ^boat 1
        ^types 1)}

Proposição 3.

sp {mac*propose*operator*move-mac-boat11
   (state <s> ^name mac
              ^ << right-bank left-bank >> <bank>)
   (<bank> ^missionaries > 0
           ^cannibals > 0
           ^boat 1)
-->
   (<s> ^operator <o> + =)
   (<o> ^name move-mac-boat
        ^bank <bank>
        ^missionaries 1
        ^cannibals 1
        ^boat 1
        ^types 2)}

IV. Regras de aplicação dos operadores.

A aplicação dos operadores segue o seguinte:

- Caso exista um operador selecionado para um dado tipo de pessoa e um número correspondente, subtrair este da margem onde está o barco e adicionar na margem oposta. Além disso, passar o barco para a outra margem.

Escrevendo essa regra para aplicação, temos:
 

sp {apply*move-mac-boat
   (state <s> ^operator <o>)
   (<o> ^name move-mac-boat
        ^{ << missionaries cannibals boat >> <type> } <number>
        ^bank <bank>)
   (<bank> ^<type> <bank-num>
           ^other-bank <obank>)
   (<obank> ^<type> <obank-num>)
-->
   (<bank> ^<type> <bank-num> -
   (- <bank-num> <number>))
   (<obank> ^<type> <obank-num> -
   (+ <obank-num> <number>))}

V. Monitoramento de operadores selecionados e estados. 

Aqui criamos uma regra para monitorar os estados em cada margem do rio e o operador selecionado:

sp {monitor*move-mac-boat

   (state <s> ^operator <o>)

VI. Regra de reconhecimento de objetivo.

É necessário a criação de uma regra que identifica que o objetivo foi atingido, essa regra é a seguinte:

- Caso o número de missionários e canibais em uma margem do rio no estado desejado seja o igual ao do estado atual, escrever que o problema foi resolvido e parar.

VII. Regra de reconhecimento de fracasso.

Uma vez que um estado de fracasso (número de canibais exceder o de missionários em uma das margens) pode ser atingido antes do estado desejado, devemos escrever também uma regra para identificar esse evento:

- Caso exista mais canibais que missionários E exista pelo menos um canibal em uma das margens, escrever que o programa falhou e parar.

Numa primeira execução do programa, verificamos que ele levou 54 passou para resolve-lo, e 14 vezes atingiu um estado de falha onde o número de canibais excedeu o de missinário em uma das margens do rio. Nota-se que existe uma grande chance de atingir um estado de falha antes de atingir o estado de sucesso desejado:

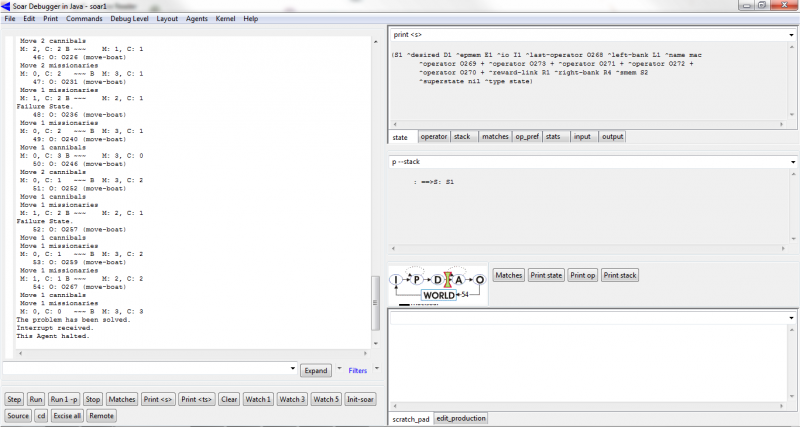
VIII. Regras de controle de busca.

No programa escrito até o momento, quando um estado de falha é atingido o programa o programa para. Porém podemos adicionar a opção de quando atingirmos um estado inválido retornarmos ao estado anterior e continuar trabalhando no problema a partir daquele ponto.

Para isso ser possível é necessario relembrar qual era o último estado. Desta forma, sao escritas duas regras para o último operador, uma que vai lembrar as propriedades do operador que move apenas um tipo de individuo, e outra que vai para quando movemos um canibal e um missionário:

- Caso um operador seja selecionado para mover apenas um tipo de indivíduo, entao crie uma nova augmentação do estado "last-operator" contendo a margem do barco, o tipo dos indivíduos sendo movidos, a quantidade, e a informação que temos apenas um tipo de indivíduo sendo movido.

- Caso um operador seja selecionado para mover dois tipos de indivíduos, então crie uma nova augmentação do estado "last-operator" contendo a margem do barco, e a informação que dois tipos de indivíduo estão sendo movidos.

Convertendo em regras SOAR temos:

A regra para remover memórias antigas deve apenas testar se a margem do barco na memória salva "last-operator" não corresponde à margem atual que o barco se encontra, isso porque cada vez que um operador é aplicado o barco é movido:

- Caso o operador move-mac-boat seja selecionado e o barco em "last-operator" não esteja na mesma margem do barco no estado atual, então remova o elemento "last-operator" da memória de trabalho.

Também é necessário criar regras que irão desfazer um operador caso este leve a um estado de falha. Por isso é necessario alterar a regra de identificação de falha para não parar o programa, e sim adicionar o atributo falha a este estado:

- Caso exista mais canibais que missionários E pelo menos um missionário em qualquer margem do rio, então criar augmentação para aquele estado com valor "TRUE".

Além disso, devem existir regras que dão preferência a operadores que desfazem o último operador quando este leva a um estado de falha. Novamente são necessárias duas regras, uma para quando move-se apenas um tipo de indivíduo e outra para quando move-se ambos:

- Caso o estado atual é de falha e o último operador é o inverso de um operador proposto, dê preferência àquele.

Essa regra em SOAR para ambos os casos é escrita da seguinte forma:

O problema com as regras incluídas até agora é capaz de resolver o problema, porém irá provavelmente ser muito ineficiente pois permite selecionar o mesmo operador que levou a um estado de falha logo após este ser desfeito. Para evitar isso são incluidas regras que evitam desfazer o último estado quando este estado não é um estado de falha:

- Caso o estado atual não é um estado de falha e o operador anterior é o inverso do operador proposto, então evitar aquele operador.

Com essas regras chegamos a forma final do programa MAC. Executando podemos ver mais detalhes da seleção de operadores quando atinge-se um estado de falha e o retorno a estados anteriores.

Tutorial 5 - Planejamento e Aprendizado

O tutorial 5 trás tecnicas para utilizar subgoals com o intuito de planejar e fazer com que o agente aprenda utilizando o chunking. Essa tecnica faz com que os problemas sejam resolvidos de forma mais eficiente, chegando no objetivo mais rapidamente.

Utilizando um planejamento para prever o resultado da aplicação de um operador antes de efetivamente aplica-lo se torna interessante quando um programa interage com o mundo exterior. Na primeira parte dessa aula, o resolução do problema era interna ao Soar, e dessa forma era possível retornar a um estado anterior quando atingissemos um estado de falha. Isso já não é possível em um agente que interage com o mundo exterior. 

O planejamento no Soar surge da detecção de impasses e do mecanismo de criação de subestados estudado anteriormente. O Soar automaticamente cria um sub-objetivo sempre que as preferências representam um conhecimento insuficiente no procedimento de tomada de decisão. Esse procedimento pode escolher um operador se existe um operador claramente preferível ou vários operadores indiferentes. Como nas regras escritas anteriormente sempre foi utilizado um indicador de preferencia indiferente, o procedimento de decisão selecionava aleatóriamente entre os operadores.

Desta forma, para começarmos a utilizar o planejamento no sistema Soar, deveremos eliminar o indicador de indiferença e utiliza-lo apenas quando não existir informação de qual operador é o melhor. Começaremos utilizando essas tecnicas no problema das jarras (water jug problem).

Problema do Water Jug

Reescrevendo agora o operador fill do water jug sem o indicador de preferência indiferente e rodando obtivemos:

Na primeira tomada de decisão após a utilização tivemos os seguintes operadores propostos (encher uma ou outra jarra):

Agora os operadores não possuem os indicadores de indiferença (=) e a execução chega a um impasse:

O objetivo desses operadores de avaliação é avaliar cada operador proposto em termos de fracasso, sucesso ou uma analise númerica da chance de sucesso de cada um.

Essas avaliações então serão traduzidas em preferências para os operadores propostos e quando preferências suficientes forem criadas para selecionar um operador, o subestado de impasse será automaticamente removido da memória de trabalho.

Como em qualquer problema trabalhado em Soar, temos que definir os seguintes conhecimentos para modelar o problema, levando agora em conta os operadores de avaliação:

I. Representação de estados

Agora deve se considerar também a representação objetos utilizados para avaliação com operadores.

II. Regra de criação do estado inicial

Uma vez que o estado inicial surge como um subestado, um estado inicial é gerado automaticamente.

III. Regras de proposição de operadores

O único operador é o operador de avaliação e deve ser proposto para todos os operadores que gerem empate na fase de seleção.

IV. Regras de aplicação de operadores

O operador de avaliação é implementedo de forma hierárquica. Portanto a aplicação de operadores envolve um subestado e operadores para esse subestado.

V. Regras de monitoramento de estado e operadores

VI. Regra de reconhecimento do estado desejado

VII. Regra de reconhecimento de falha

VIII. Regras de controle de busca