- Aula 1 - Introdução
- Aula 2 - SOAR: Tutorial 1
- Aula 3 - SOAR: Tutorial 2
- Aula 4 - SOAR: Tutorial 3
- Aula 5 - SOAR: Tutoriais 4 e 5
- Aula 6 - SOAR: Tutoriais 7, 8 e 9
- Aula 7 - SOAR: Controlando o WorldServer3D
- Aulas 8 e 9 - Clarion
- Aulas 10 e 11 - Clarion: Controlando o WorldServer3D
- Aula 12 - LIDA 1: Entendendo a Arquitetura
- Aula 13 - LIDA 2: Exemplos de Implementação Prática
- Aulas 14 e 15 - Projeto: LIDA - Controlando o WorldServer3D
You are here
Aula 5 - SOAR: Tutoriais 4 e 5
SOAR: Tutoriais 4 e 5
Objetivo
Desenvolver as atividades nos Tutoriais 4 e 5 do Soar. Essas atividades envolvem técnicas clássicas de Inteligência Artificial, como buscas, planejamento e uma técnica de aprendizagem chamada de chunking.
Relatório das Atividades
Atividade 1
As atividades do Tutorial 4 apresentam o uso do Soar para resolver o problema "Missionários e Canibais", cujo enunciado é:
Três missionários e três canibais chegam a um rio. Na margem do rio há um bote que pode ser usado por uma ou duas pessoas de cada vez. Esse bote deve ser usado para atravessar o rio de tal forma que o número de canibais não exceda o de missionários em cada uma das margens (embora possa haver apenas canibais em uma das margens). Como missionários e canibais podem atravessar o rio com sucesso?
"Missionários e Canibais" é um problema clássico em Inteligência Artificial e está na categoria cuja solução se baseia na busca no espaço de soluções do problema.
Os passos para a criação de um programa Soar para resolver o problema são:
Definição de como representar o estado
O primeiro passo para criar um programa Soar que resolva o problema é decompô-lo em seu espaço de soluções (a representação do estado e os operadores pertinentes) e em sua definição (estado inicial e estado desejado). É interessante notar que no espaço de soluções há estados de falha (onde há mais canibais do que missionários em uma das margens do rio) que devem ser evitados.
Os aspectos importantes que devem ser representados pelos estados são:
- O número de missionários em cada margem do rio
- O número de canibais em cada margem do rio
- A margem do rio onde o bote está
O mais adequado, permitindo a criação de regras mais gerais, é representar cada aspecto separadamente usando objetos estruturados. Assim, o estado contém dois objetos (left-bank e right-bank), cada um representando uma das margens do rio. Cada um desses objetos contém 3 subobjetos (missionaries, cannibals e boat), representando o número de missionários, o número de canibais e se o bote está ou não na margem repesentada, e, adicionalmente, um atributo representando a outra margem (other-bank), com o objetivo de simplificar o processamento (Fig. 1.1).
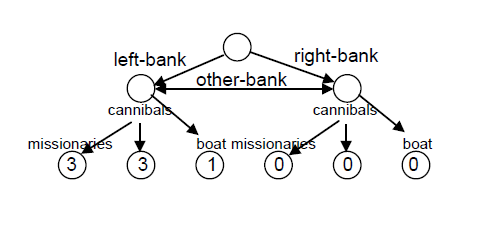 |
| Fig. 1.1 - Representação dos estados |
Criação do estado inicial
A criação do estado inicial, adicionando os elementos com os valores adequados é semelhante ao que foi usado na solução do Problema dos Jarros de Água, no Tutorial 1. O código para o Soar é mostrado na Fig. 1.2. Deve ser notada a inclusão de um atributo adicional para representar o estado desejado (desired).
 |
| Fig. 1.2 - Criação do estado inicial |
Definição das regras de proposição de operadores
Os operadores devem mover um ou dois indivíduos (missionários ou canibais) de uma margem para a outra do rio. E é mais fácil quebrar os operadores em três classes:
- mover um missionário ou um canibal para a outra margem, testando se há pelo menos um indivíduo do mesmo tipo na margem com o bote
- mover dois missionários ou dois canibais para a outra margem, testando se há pelo menos dois indivíduos do mesmo tipo na margem com o bote
- mover um missionário e um canibal, juntos, testando se há pelo menos um indivíduo de cada tipo na margem com o bote.
A Fig. 1.3 mostra as regras de proposição de operadores generalizadas, para cada uma dessas classes.
 |
| Fig. 1.3 - Regras de proposição de operadores |
Definição das regras para aplicação dos operadores
A aplicação dos operadores deve alterar os valores para missionários, canibais e bote em cada uma das margens, decrementando na margem de origem e incrementando na margem de destino. O operador é testado para verificar a correspondência do número de indivíduos a serem movidos, de acordo com as classes propostas. As ações rejeitam os valores correntes e adicionam os novos valores.
A Fig.1 .4 - mostra a regra de aplicação de operadores, generalizada.
 |
| Fig. 1.4 - Regras de aplicação de operadores |
Definição das regras para monitoração de estados e operadores
As regras mostradas na Fig. 1.5, permitem a monitoração de estados e operadores de forma a auxiliar a compreensão de como o programa SOAR se comporta durante a solução do problema.
 |
| Fig. 1.5 - Regras para monitoração de estados e operadores |
Definição da regra para reconhecimento do estado desejado (solução para o problema)
É importante definir uma regra que permita reconhecer quando a solução para o problema for encontrada. A regra na parte superior da Fig. 1.7 imprime a mensagem de que o problema foi resolvido e para o programa quando o estado desejado é alcançado. No entanto, o desenvolvimento até agora não garante que o programa não passe por um estado inválido e resolva o problema de forma incorreta.
 |
| Fig. 1.6 - Regras para reconhecimento do estado desejado e para deteção de estado de falha |
Definição da regra para deteção de estado de falha
A parte inferior da Fig. 1.6 mostra uma regra para a deteção de estados de falha, que no caso do problema em questão, ocorre quando o número de canibais supera o de missionários em uma das margens do rio. Essa regra imprime uma mensagem de estado de falha e registra a situação no estado corrente. Esse registro será usado adiante para o controle de busco no espaço de soluções para o problema.
Definição de regras para controle da busca no espaço do problema (desfazer o último operador)
Uma solução para evitar que o programa pare ao encontrar um estado de falha seria fazer com ele reiniciasse a busca a partir do estado inicial. No entanto, uma solução mais inteligente é desfazer a última operação que levou ao estado de falha e buscar um outro caminho. Para isso, é necessário armazenar a última operação e definir preferências de forma a evitar desfazer o último operador preferindo desfazer o operador que levou ao estado de falha. Também, é necessário evitar desfazer o último operador que não levou a um estado de falha. Regras para isso são mostradas nas Fig. 1.7 e Fig. 1.8.
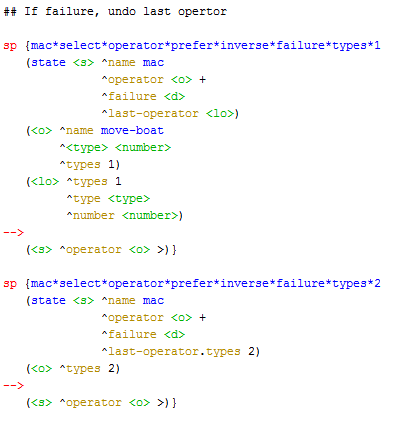 |
| Fig. 1.7 - Regras para controle de busca |
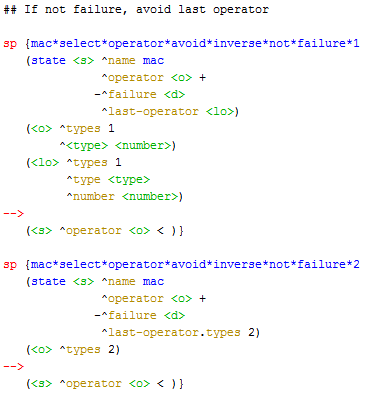 |
| Fig. 1.8 - Regras para controle de busca |
Observa-se que com esse conjunto de regras o programa alcança a solução para o problema mas ainda de uma forma não muito eficiente. A próxima atividade mostrará técnicas para aumentar a eficiência na solução de problemas.
Atividade 2
As atividades do Tutorial 5 apresentam como construir programas Soar que usam objetivos intermediários (subgoals) para planejar (look-ahead planning) e aprender (chunking learning type). Em uma forma simples de planejamento look-ahead, um agente irá tentar a execução e a avaliação de diferentes operadores, internamente, antes de aplicá-los na tarefa corrente. Isso é muito relevante em problemas onde o agente interage com o mundo real e que não há a possibilidade de desfazer uma ação se um estado de falha for encontrado. Adicionalmente o planejamento permite comparar operadores alternativos com base nos estados que esses produzem. O chunking constrói regras que sumarizam as comparações e avaliações que ocorrem na busca look-ahead de forma que, no futuro, possam ser disparadas sem a necessidade de excecutar o processo de busca novamente; convertendo deliberação em reação.
Planejamento no SOAR surge dos mecanismos de deteção de impasse e criação de substados. O SOAR automaticamente cria um objetivo intermediário sempre que as preferẽncias forem insuficientes para que o pro selecione um operador. Isso indica que o conhecimento disponível é insuficiente para uma tomada de decisão e que a solução para o problema ainda não foi encontrada. O planejamento é então mais uma fonte de conhecimento que pode ser usada sempre que o conhecimento codificado diretamente nas regras for insuficiente para uma tomada de decisão. O processo de decisão só pode escolher um operador se houver um claro vencedor ou se houver múltiplos operadores cuja seleção seja indiferente. No entanto, a preferência indiferente só deve ser usada somente quando a escolha de qualquer operador for indiferente e não quando não houver informação suficiente para escolher o melhor operador. Assim, o primeiro passo para que o planejamento seja invocado é eliminar a preferência indiferente das regras de proposição de operadores.
Quando não há informação suficiente para escolher entre os operadores propostos o SOAR gera um impasse do tipo tie impasse. O SOAR cria um novo subestado é criado sempre que ocorre um impasse de forma a permitir que a situação seja alterada e o impasse resolvido. No caso do tie impasse, o objetivo é determinar qual é o melhor operador da tarefa a ser aplicado no estado corrente. Isso pode ser alcançado selecionando e avaliando operadores no subestado, um para cada operador da tarefa. O objetivo é criar uma avaliação para os operadores de tarefa de forma simbólica (falha, sucesso) ou numérica (probabilidade de sucesso). Essas avaliações são convertidas em preferências para os operadores. Uma vez que sejam criadas preferências suficientes para permitr a seleção de um operador, esse será selecionado e o substado será automaticamente removido da memória de trabalho.
Os programas para a solução dos problemas dos Jarros D'Água (Water Jug) e dos Missionários e Canibais foram alterados para utilizar os mecanismos de planejamento e aprendizado.
A comparação de execuções do programa SOAR para a solução do problema dos Jarros D'Água (Water Jug), com e sem a utilização de planejamento e aprendizado, é sumarizada na tabela a seguir.
| Execução | Básico | Look-ahead + Chunking |
| 1 | 136 | 81 |
| 2 | 280 | 7 |
| 3 | 279 | 7 |
| 4 | 480 | 7 |
| 5 | 281 | 7 |
| 6 | 171 | 7 |
| 7 | 437 | 7 |
| 8 | 408 | 7 |
| 9 | 232 | 7 |
| 10 | 269 | 7 |
A comparação da execução do programa SOAR para a solução do problema dos Missionários e Canibais, com e sem a utilização de planejamento e aprendizado, é sumarizada na tabela a seguir.
| Execução | Básico | Look-ahead + Chunking |
| 1 | 210 | 153 |
| 2 | 40 | 12 |
| 3 | 98 | 12 |
| 4 | 84 | 12 |
| 5 | 46 | 12 |
| 6 | 20 | 12 |
| 7 | 302 | 12 |
| 8 | 104 | 12 |
| 9 | 28 | 12 |
| 10 | 188 | 12 |
Para ambos os problemas, o uso das técnicas de planejamento e aprendizado permitiu encontrar a melhor solução já na segunda execução.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer
