You are here

Home » Courses » IA006 » Apresentação de Atividades » Apresentação de Atividades - Turma 2013 » Aluno 2 » Aula 5 - 05/04/2013 - Tutorial 4 e Tutorial 5

Atividade 1: execução do tutorial 4 - problema dos Missionários e Canibais

published by aluno2 on Tue, 04/16/2013 - 20:52
Esta atividade corresponde em desenvolver o tutorial 4 do Soar.
 
 
Neste tutorial é proposto a soluçao do problema dos missionários e canibais, cuja descrição é a seguinte:
 
Estão numa margem de um rio 3 missionários, 3 canibais e um barco que pode levar até 2 pessoas. O objetivo é transportar todos as 6 pessoas para o outro lado, nunca deixando em nenhuma margem um número mairo de canibais do que missionários.
 
 
Tal como o problema do jarro de água, corresponde a uma resolução que ocorre simplesmente por busca interna.
 
O tutorial propõe uma sequência para resolução do problema usando o Soar, que é descrita a seguir.
 
 
Descrição do problema
 
O primeiro passo proposto é decrever o problema em suas características, respondendo a algumas questões:
 
  1. Como representar os estados: posição dos canibais e missionários nas 2 margens do rio, posição do barco. A regra Soar de inicialização do problema ilustra a representação escolhida:

 

  1. Estado inicial: todos os 3 canibais e 3 missionários estão do mesmo lado do rio; na implementação, foi escolhida a margem esquerda como a inicial.
  2. Regras de proposição de operadores: mover até 2 pessoas - em qualquer combinação - para o outro lado do rio.
  3. Regra para reconhecimento do estado final: todos as 6 pessoas atravessaram o rio. Na regra de inicialização existe a criação de uma extensão "^desired" com o "gabarito" do estado final. Esse "gabarito" é constantemente verificado pela regra representada abaixo, que dispara sempre que a representação do estado atual é alterada:

 

  1. Regras para reconhecimento de estados inválidos: quando, em qualquer uma das margens do rio, o número de canibais for maior que o número de missionários. Essa condição inválida é constantemente verificada toda vez que o estado atual é alterado, através da seguinte regra:
 
 
 

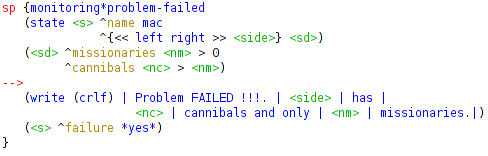
Regras para operadores

 
Segundo o tutorial, é um objetivo conseguir mapear a DESCRIÇÃO DO PROBLEMA em um espaço de conhecimento distinto da forma de RESOLUÇÃO, ou seja, dos operadores.
 
Por esse motivo são propostos operadores que não testam diretamente o estado resultante de maneira a poder evitar estados inválidos, como é possível verificar nos operadores abaixo:
 
 
 
Uma vez que os operadores simplesmente verificam as condições mínimas para a sua aplicação - no caso, número suficiente de canibais e missionários, assim como a presença do barco - a cada passo de resolução do problema serão propostos inúmeros operadores, muitos dos quais levarão a estados inválidos ou a estados já trabalhados em passos anteriores. Mas como não se deseja evitar esses operadores diretamente em suas regras de proposição, todos eles devem ter a preferência de indiferença e regras adicionais precisarão ser criadas para essas situações problemáticas.
 
Para a situação de estaods inválidos, é necessário retornar ao estado anterior, aplicando a operação inversa da operação que levou até o problema; isso pode ser feito de uma maneira bastante interessante, através da seguinte regra de seleção:
 
 
Como a cada rodada todos os operadores possíveis são propostos, para aplicar o operador inverso no caso de falha ("^failure *yes*") basta indicá-lo como o mais preferencial, que é justamente o que as regras acima fazem.
 
Algo similar pode ser feito para se evitar que seja aplicada a regra inversa num caso em que o estado atingido foi válido, o que causaria um atraso na resolução do problema:
 
 
Neste caso, as regras que desfazem o operador anterior são marcadas como as menos prioritárias.
 
Um detalhe importante é que a criação dos operadores deve se preocupar com o fato de que como será necessário manipulá-los a partir de outras regras, de forma a direcionar o resultado, quanto mais genéricos forem os operadores, menor será o trabalho dessa manipulação, a qual poderá fazer uso de regras comuns. Isso é bem ilustrado no caso da regra de aplicação dos operadores:
 
 
 
Dessa maneira, embora aparentemente não seja necessária a inclusão o barco dentro do operador, a máxima generalização é possível com a sua inclusão: é possível assim aplicar em paralelo o operador para cada tipo de elemento sendo transportado de uma vez só: quando o barco for movido de um lado para o outro, todos os operadores propostos vão deixar de valer - daí a necessidade de fazer tudo em paralelo.
 
O atributo "types" é necessário para a etapa da INVERSÃO do operador, uma vez que não é possível saber diretamente se o movimento é para 1 ou 2 tipos de pessoas, já que a aplicação dos operadores é feita tipo a tipo.
 
 
 

Conclusão

 
Em 10 testes o programa desenvolvido resolveu o problema com uma média de 185,4 ciclos do Soar; a resolução mais rápida levou 40 ciclos e a mais demorada levou 306 ciclos.
 
 
A partir da execução deste tutorial é possível listar os seguintes pontos:
 
  1. Separação da descrição do problema da resolução do problema.
  2. Explora novamente abordagem de resolução dos problemas a partir da exploração de todas as possibilidades.
  3. Explora a criação de regras compactas.
 
 
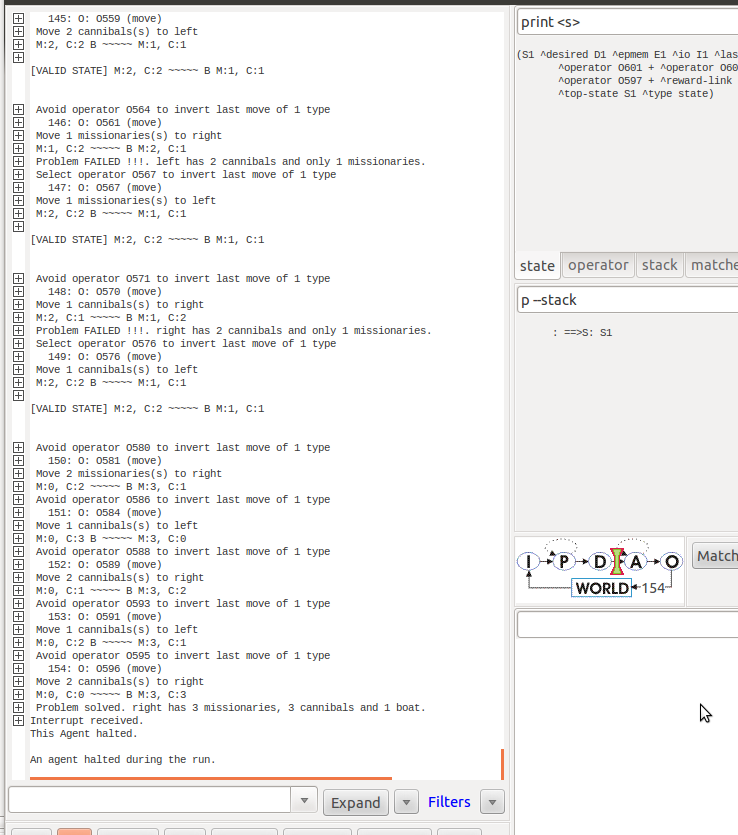
Exemplo de resolução do problema
 

Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer