Aula 5 - SOAR Tutorial 4 e 5 -

Atividade 1 - Tutorial 4 - Resolução mais simples de problemas

Padres e Canibais

Nesse tutorial vamos resolver um outro problema clássico de IA: Padres e canibais.
Eis a premissa do problema:

Três padres e três canibais foram à um rio. Há um barco do lado deles do rio que pode ser usado para transportar uma ou duas pessoas. Este barco deve ser usado para travessia do rio de modo que nunca haja mais canibais que padres de um dos lados do rio, embora os canibais possam ficar sozinhos em um nos lados. Como eles atravessam o rio com sucesso?

O primeiro passo para a criação de um programa em Soar que resolve o problema é a decomposição do problema em estados e operadores e representar o estado final desejado. Como podemos observar no diagrama parcial abaixo, há vários estados ilegais onde falharíamos caso seguíssemos por eles:

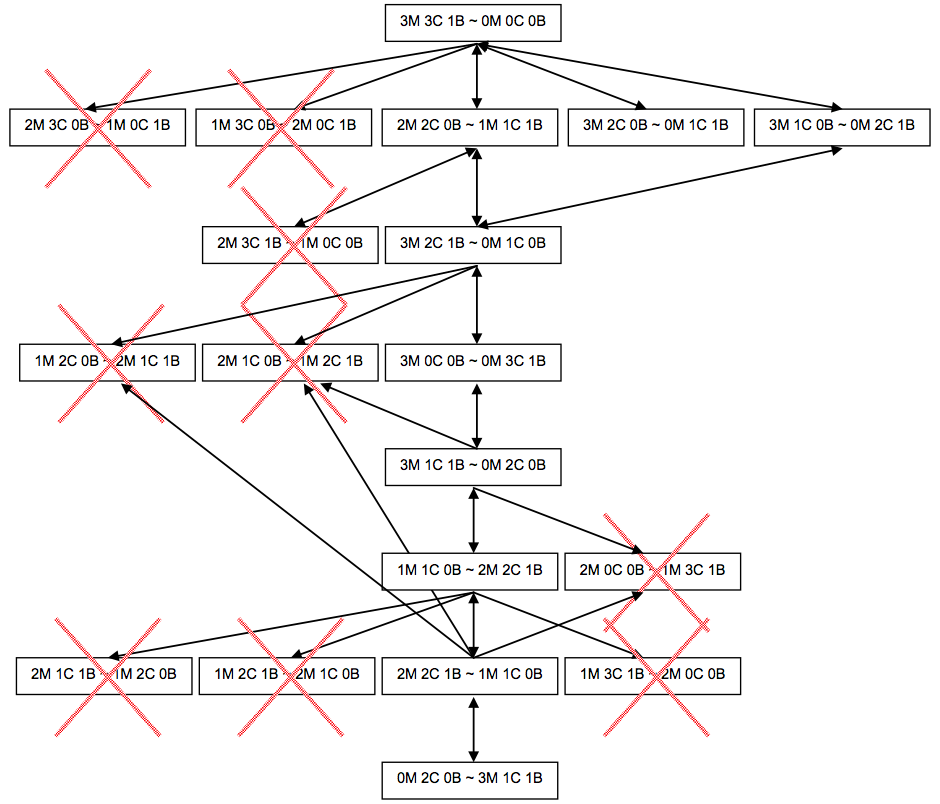
Representação de estados

Para representar os estados do espaço do nosso problema, temos que pensar no que é pertinente à resolução do problema. Como por exemplo:

• O número de padres de cada lado do rio
• O número de canibais de cada lado do rio
• O lado do rio no qual está o barco

Para tornar possível a criação de regras mais genéricas, vamos usar representações estruturadas dos nossos objetos, que por instância são: padres, missionários, barco e rio.
Vamos seguir a seguinte estrutura:

A figura ilustra inclusive nosso estado inicial, que será todos os padres, todos os canibais e o barco do lado esquerdo do rio. A representação "other-bank" pode ser incluída para que possamos verificar o lado oposto mais facilmente.

Estado inicial e operadores

O tutorial segue com a criação do estado inicial, assim como fizemos no problema do WaterJug:

Os operadores propostos para resolução do problema movem de 1 a 2 indivíduos através do rio e são quebrados em três classes:

• Mova um padre ou canibal para o outro lado -> Verifique que há ao menos um do dado tipo em terra no barco.
• Mova dois padres ou dois canibais para o outro lado -> Verifique que há ao menos dois do dado tipo em terra no barco.
• Mova um padre e um canibal juntos para o outro lado -> Verifique que há ao menos um de cada tipo em terra no barco

O primeiro operador então deve mover um padre ou um canibal para o outro lado do rio, o tutorial começa escrevendo a regra em Soar bem especificamente e depois abstrai partes das condições como variáveis, a regra final fica como segue:

Com essa regra podemos entender que desde que haja do rio onde está o barco algum canibal ou padre, podemos propor que um deles seja levado para o outro lado.

O segundo operador move dois padres ou dois canibais. O que requer uma pequena mudança da primeira regra para essa, temos apenas que testar se há mais de um padre ou canibal e aumentar o número de pessoas sendo transportadas para 2:

Nessa regra propomos mover duas pessoas do mesmo tipo, desde que do lado do rio onde está o barco haja mais de um padre ou canibal.

O terceiro operador, ainda é bastante similar aos dois primeiros, única diferença é que agora estaremos transportando um padre e um canibal, desde que do lado do rio onde está o barco haja padres e canibais:

Aplicação de Operadores

Para a aplicação dos operadores devemos modificar a representação do estado atual. Para movermos as pessoas de um lado para o outro do rio, não precisamos representar quais estão no barco, apenas que elas se moveram de um lado do rio para o outro. Assim, basta incrementar o número de padres e/ou canibais no lado do rio para qual o barco está direcionado, e decrementar o número do lado de onde o barco partiu.

Essa regra em Soar pode ser um pouco complexa por conta do número de variáveis, vamos analizar:

Essa regra testa se o operador escolhido foi o "move-mac-boat", então atribui a variavel <type> o tipo de objeto se movendo, podendo ser uma das extensões: padre, canibais ou barco. A variavel <number> terá o número de entidades do tipo <type> e <bank> e <obank> apontam cada uma para um lado do rio. A aplicação desse operador subtrai o número de pessoas em movimento de um lado do rio e soma no lado oposto.

Para que seja possível acompanhar o andamento da resolução do problema, vamos escrever regras de monitoramento que vão imprimir no debugger o operador escolhido, isto é, que tipo de pessoa vamos movimentar e em qual quantidade. Além disso, vamos imprimir o estado de cada lado do rio:

Reconhecimento de estados falhos e final

O próximo passo é escrever as regras de reconhecimento do estado desejado, isto é, se todos os padres e todos os canibais estão do outro lado do rio, o que é bastante direto:

Se rodarmos essa regra juntamente com as previamente escritas, veremos que o programa irá parar em algum momento, porém, possivelmente terá passado por estados inválidos e resolvido o problema de maneira errada.

Para evitar que esse cenário aconteça, vamos detectar estados inválidos. Nas regras que temos até agora, nunca testamos se o número de canibais é maior que o de padres de um mesmo lado do rio, o que representa exatamente um estado inválido. Com a seguinte regra iremos reconhecer esse estado e parar o programa:

Ao rodar o programa com mais essa regra, invariavelmente ele irá parar com uma falha, por conta da alta chance de encontrar um estado inválido.

Desfazendo o último operador

Poderíamos reiniciar o programa a cada vez que encontrássemos um estado inválido e esperar que novos caminhos fossem tentado, mas isso não é muito eficiente. O que precisamos é criar uma memória do último operador utilizado.
Para isso precisaremos escrever duas regras, uma para guardar o último operador, pois temos um operador para carregar apenas um tipo de pessoa e outro para carregar mais de um tipo.

A regra no programa Soar se parecerá com a seguinte:

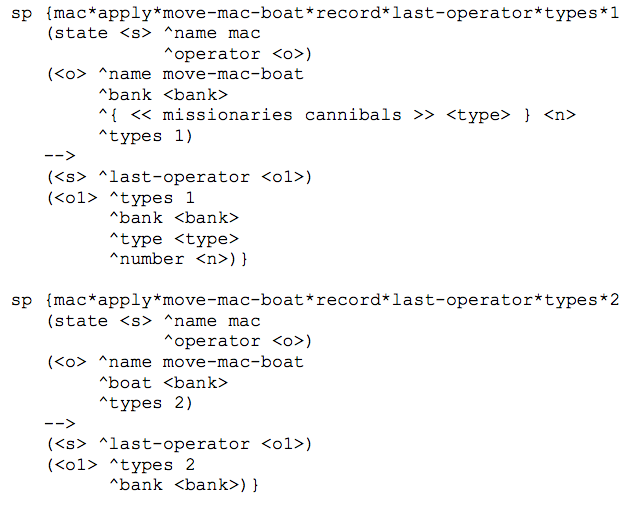
Na primeira regra, se um operador foi selecionado para mover um tipo de pessoa, então criamos uma extensão do estado (last-operator) com o lado do rio em que o barco está, o tipo de pessoa sendo transportada, o número e que há apenas um tipo de pessoa sendo transportada.

Na segunda regra, se um operador foi selecionado paramover dois tipos de pessoas, então criamos uma extensão do estado (last-operator) com o lado do rio em que o barco está e que há dois tipos de pessoas em transporte.

O próximo passo é ter uma regra que remove essa memória quando não for mais verdade:

Nessa regra, se o operador move-mac-boat está selecionado e o último operador não corresponde ao lado em que se encontra o barco, então removemos a memória do último operador.

Feito isso, podemos escrever regras para desfazer o último operador. Portanto, é necessário modificar a regra de detecção de falha para que essa não pare o programa, e sim, apenas crie uma extensão no estado indicando falha.

Essa regra disparará somente quando um estado ilegal for atingido e não é parte da aplicação de um operador. Por isso, irá retrair e remover a extensão de falha automaticamente se o estado mudar e não for mais ilegal.

Agora teremos regras de controle de busca para preferir regras que desfaçam o último operador quando houver uma falha. Com isso nosso programa consegue resolver o problemas, mas para uma solução mais robusta, adicionaremos regras que inibam o programa de escolher um operador que seja o inverso do último operador, pois se estamos fazendo e desfazendo em seguida estamos desperdiçando uma aplicação de operador.

Para o código fonte usado na execução, clique aqui. Com todas essas regras, obtemos a seguinte saída no debugger:

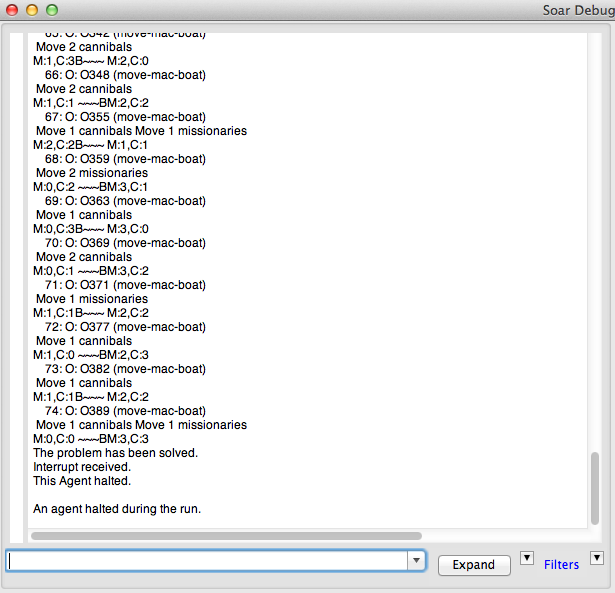
Atividade 2 - Tutorial 5

Planejamento e Aprendizado

Nesse tutorial, vamos aprender sobre como programas Soar podem olhar adiante e planejar ações antes de executá-las. E então vamos fazer pequenas modificações nos problemas do Water-Jug e do Missionaries And Cannibals. O planejamento acelera a resolução do problema gerando regras de controle de busca.

Em alguns casos, como o problema dos Padres e Canibais, tinhamos uma regra que desfazia uma ação que nos levara a um estado indesejado, mas em caso de programas que agem em um mundo nem sempre podemos desfazer ações, por isso precisamos testar regras internamente entes de nos comprometermos a aplicá-las.

Muitos sistemas de planejamento têm um ciclo de dois estágios de planejamento e execução. Eles sempre planejam e depois executam o planejado passo-a-passo. Em Soar a abordagem é um pouco diferente, iremos planejar sob demanda, usando quaisquer conhecimentos disponíveis no estado em que estivermos. Isso torna nosso processo de planejamento mais flexível e possibilita que a resolução de um problema seja parte da resolução de outro.

Nosso estudo de planejamento vai acontecer em paralelo com o de resolução de problemas. Vamos começar com o Water-Jug.

Revisitando o Water-jug

O planejamento em Soar emerge do mecanismo de detecção de impasse e criação de subestado. Toda vez que o mecanismo de decisão não consegue escolher um operador baseado no conhecimento atual, um novo subestado é gerado para uma nova resolução de problema.
O mecanismo de decisão só consegue escolher um operador caso haja um de preferencia dominante sobre todos os outros, ou quando todos os operadores têm preferencia indiferente, o que causa a escolha aleatória.
Porém, a prefenrecia indiferente deve ser usada quando é sabido que qualquer um dos operadores pode ser escolhido, ao invés de quando não sabemos qual é o melhor. Sendo assim, o primeiro passo para adicionarmos planejamento ao nosso Water-Jug existente é remover as preferências indiferentes.

Abaixo a proposição do operador fill sem a preferência indiferente:

Se rodarmos novamente o Water-Jug com essa regra modificada, veremos que em poucos passos o programa gerará um impasse de empate, ou tie impasse.

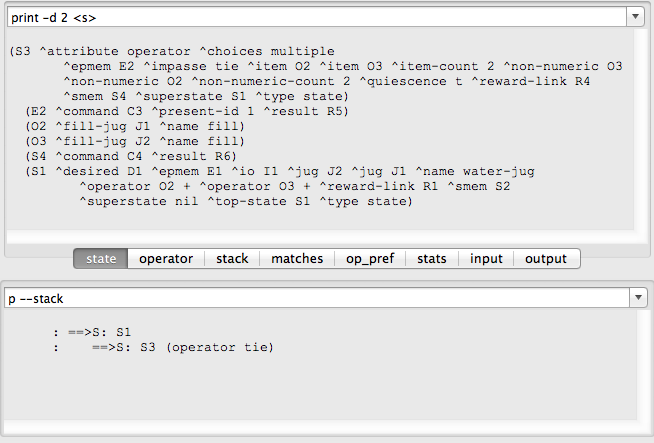
Para o tie impasse, o objetivo é determinar qual operador é o melhor a ser aplicado no estado atual. Para isso, selecionaremos e aplicaremos operadores de avaliação no subestado, um para cada operador da tarefa. O propósito desses operadores de avaliação é justamente gerar avaliações sobre os operadores da tarefa, como falha, sucesso ou uma avaliação numérica da probabilidade de sucesso. Essas avaliações serão então convertidas em preferencias para os operadores. Uma vez que as preferencias criadas sejam suficientes, o operador será normalmente selecionado e o subestado será removido. É possível que depois de avaliar um conjunto parcial dos operadores empatados, preferências suficientes serão criadas para quebrar o empate. Por exemplo, se um operador é avaliado e foi determinado que ele vai direto ao estado desejado, uma preferência de "o melhor" pode ser criada para ele, quebrando assim, o empate.

Essas avaliações só são possíveis aplicando operadores em cópias internas do estado atual, onde podemos testar se o estado gerado é de falha, inicial ou desejado.

Iremos tratar o problema de seleção como qualquer um outro, porém, pode ser bastante complexo desenvolver funções de avaliação para problemas específicos, por isso com o release do Soar temos algumas regras padrões criadas para nos ajudar nessa situação. Vamos incluí-las em nosso projeto, atrás dos comandos pushd e popd no nosso arquivo soar mais geral do projeto:

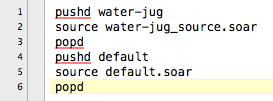
A pasta 'default' foi copiada de dentro dos tutoriais para a pasta onde estão os arquivos de projeto do Water-Jug.

Criando o Estado Inicial de Seleção

Para que seja possível implementarmos regras de avaliação, algumas extensões do estado pertinentes ao nosso problema específico têm que ser copiadas para o subestado criado pelo Soar frente a um impasse. Para isso, elaboramos o estado com uma referência para o espaço do problema, onde configuraremos o que será copiado para o subestado a ser criado, de forma que tenhamos todas as informações necessárias para trabalhar nossas avaliações.
Nas regras padrões fornecidas pelo Soar, temos regras que testarão essa configuração do espaço do problema e irão conduzir a criação dos nossos subestados.
Vamos analisar a regra a seguir:

A extensão ^default-state-copy com o valor 'yes' não permite que nenhuma extensão seja copiada automaticamente, e a extensão ^two-level-attributes com valor 'jug' configura a cópia com profundidade "dois" da extensão "jug" do nosso estado.

Com essa configuração, nosso subestado ficaria assim:

// ON GOING

* As seções a seguir explicam quais as modificações necessárias, e os fundamentos para tais, para conseguirmos regras de elaboração e assim o planejamento das ações.

* Há uma seção que nos ajuda pontualmente a modificar o Missionaries and Cannibals para usar regras de elaboração, e mais tarde, uma pequena modificação para usarmos o chunking mais efetivamente. Os passos para a converção do Missionaries and Cannibals são os seguintes:

• Retirar as proposições de preferência indiferente
• Adicionar regras padrões de seleção
• Adicionar a extensão de espaço do problema e configurar a cópia do estado para o subestado
• Modificar a detecção de estado final
• Modificar detecção de falha
• Adicionar regra para detecção de estados duplicados
• Remover regras de memória do último operador aplicado

* Há uma parte sobre Chunking, que até onde entendi, é um mecanismo do Soar para aprender uma melhor resolução para o problema. O que ele faz para isso é montar estruturas que ligam operadores com o estado e o resultado da aplicação daquele operador, tendo assim, em mãos, as informações necessárias para evitar ou repetir a aplicação de um operador em dado estado.
Para utilizar chunking é necessário ativá-lo pelo comando 'learn --on'

* Postar o código modificado do Missionaries and Cannibals junto com algumas comparações com chunking e sem chunking.

Para acessar o código modificado do Missionaries and Cannibals clique aqui.

Ao executar o programa do Missionaries and Cannibals com planejamento, percebemos a a criação de subestados a cada impasse:

Ao ativarmos chunking com o comando 'learn --on' no inicio do código fonte, o programa executa mais rapidamente e resolve o problema: